Example: Fighter Aircraft Problem – Permutation Method
Fighter
Aircraft Problem
Assume that
the cardinal weight of the criteria be w = (0.2,0.1,0.1,0.1,0.2,0.3). There
are 4! = 24 alternatives to be tested:
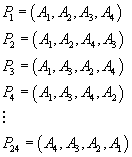
Let's test
the hypothesis 
(i.e. the ordering P4). The
matrix C4 is then:
|
|
1 |
3 |
4 |
2 |
|
1 |
0 |
0.5 |
0.6 |
0.7 |
|
3 |
0.5 |
0 |
0.8 |
0.7 |
|
4 |
0.7 |
0.2 |
0 |
0.7 |
|
2 |
0.3 |
0.6 |
0.3 |
0 |
For example,
the variant A1 is than better than A3 under criteria f1 and f6.
The element c31
we got comparing variants A3 and A1.Variant A3
is better under criterion f2 (v2=0.1), f3 (v3=0.1), f4 (v4=0.1)
and f5 (v5=0.2). The sum of weights is:
Note that the
criterion f4 price is minimal !
Then the
evaluating criterion of P4 is:
,
where 
is the
sum of upper-triangular elements of matrix C4 and 
is the sum of lower-triangular elements.
The similar C
matrices could be computed for all 24 permutations. Since the R for permutation (A3,A4,A1,A2) gives the highest
value, this order is the best.