A case study - Brewery

A brewery management prepares a production plan for the next year. Malt - the basic raw material for beer production will be produced in company's own malt-house and/or purchased at the market.

Forecasted malt need for respective quarters of the next year is as follows:
 
Period
Quantity

[tons]
1st quarter:
200
2nd quarter:
220
3rd quarter:
250
4th quarter:
160

Maximum production capacity of the own malt-house is 160 t per quarter.

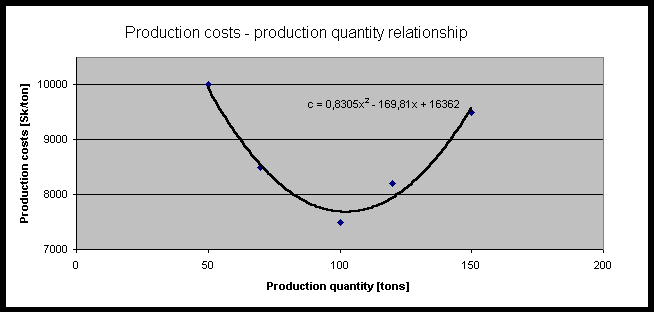
Malt production costs depend on the malt quantity produced. In previous years the following relationship was recorded:
 
Production

[tons]
Costs

[Sk/ton]
x(i)
c(i)
50
10000
70
8500
100
7500
120
8200
150
9500

Market price of the malt depends on the time of purchase. Estimated price in quarters is as follows:
 
Period
Price

[Sk/ton]
1st quarter:
8300 
2nd quarter:
8300
3rd quarter:
8200
4th quarter:
8100

Limmited budget of 2 500 000 Sk has been planned for malt purchase.

Formulate mathematical programming problem for the optimal plan of malt production/purchase with the objective of minimal costs.

Problem formulation:

Variables:

x1 - quantity of malt to be produced in the 1st quarter

x2 - quantity of malt to be produced in the 2nd quarter

x3 - quantity of malt to be produced in the 3rd quarter

x4 - quantity of malt to be produced in the 4th quarter
 
 

y1 - quantity of malt to be purchased in the 1st quarter

y2 - quantity of malt to be purchased in the 2nd quarter

y3 - quantity of malt to be purchased in the 3rd quarter

y4 - quantity of malt to be purchased in the 4th quarter

Preparatory calculations:

Relationship between malt quantity production and production costs has been investigated. A nonlinear relationship (parabola) has been used (see regression calculations in the file Brewery-QPP.xls):

c = 16361,84 - 169.805x + 0.830489x2

Quadratic programming problem:

Objective function

 min z = (16361,84 - 169.805x1 + 0.830489x12)x1 + (16361,84 - 169.805x2 + 0.830489x22)x2 + (16361,84 - 169.805x3 + 0.830489x32)x3 + (16361,84 - 169.805x4 + 0.830489x42)x4 + 8300y1 + 8300y2 + 8200y3 + 8100y4

Subject to
Malt need (production & purchase)      
1st Q.
x1
      
+ y1
      
<=
200
2nd Q.  
x2
      
+ y2
    
<=
220
3rd Q.    
x3
      
+ y3
  
<=
250
4th Q.      
x4
      
+ y4
<=
160
Malt-house production limits    
1st Q.
x1
              
<=
160
2nd Q.  
x2
            
<=
160
3rd Q.    
x3
          
<=
160
4th Q.      
x4
        
<=
160
Malt purchase        
+8300 y1
+ 8300y2
+ 8200y3
+ 8100y4
<=
2500000
x1, x2, x3, x4, y1, y2, y3, y4
=>
0

Problem has been solved by Excel's Sover - see file Brewery-QPP.xls.

Optimal solution is as follows:

x1 = 132.08 - quantity of malt to be production in the 1st quarter
x2 = 132.08 - quantity of malt to be production in the 2nd quarter
x3 = 131.53 - quantity of malt to be production in the 3rd quarter
x4 = 130.97 - quantity of malt to be production in the 4th quarter
 

y1 = 67.91 - quantity of malt to be purchased in the 1st quarter
y2 = 87.91 - quantity of malt to be purchased in the 2nd quarter
y3 = 118.47 - quantity of malt to be purchased in the 3rd quarter
y4 = 29.03 - quantity of malt to be purchased in the 4th quarter

Total production and purchase costs are: 6924975,96 Sk