1. Definition of variables

… number of barrels of BG1 used in aviation gasoline

…number of barrels of BG2 used in aviation gasoline

… number of barrels of BG1 used in motor gasoline

…number of barrels of BG2 used in motor gasoline

P … total revenue

Maximise: 

is the total amount of aviation gasoline mixed (in barrels), and since it sells at $48,50 per barrel, the revenue from this product is .Similarly, the revenue from motor gasoline is and the sum of these terms is the total revenue, P.

The fact that no more than 20,000 barrels of aviation gasoline can be sold may be represented by the following expression:



Following set of constraints is related to available amounts of blending gasolines:





x₁+x₃ represents the total amount of BG1 (the sum of the amount used in aviation gasoline, x_1, plus the amount used in motor gasoline, x₃). The first equation above states that the amount of blending gasoline BG1 used ( both in aviation and motor gasoline) must not exceed the amount available—30,000 barrels. The constraint limiting the total amount of blending gasoline BG2 to 70000 is similar.

 Another set of constraints relates to the octane ratings of the final-product gasolines. The total amount of aviation gasoline is x₁+x₂. Its octane rating will be determined by the relative amounts of x₁ and x₃ according to the following:

Octane rating of x₁ is 104; octane rating of x₂ is 94; octane rating of final product (x₁+x₂)is 102. So we get the following constraint:



Rearranging this expression in order not to have any variable in right-hand side, we have:



What is the same as: 

Similarly, for the octane rating for motor gasoline, we have:



A final set of constraints is related to the vapour pressure requirements of the

final-product gasolines. For aviation gasoline, we have:



and the vapour pressure requirement of motor gasoline is

4. Non-negativity

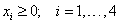
The amount of any gasoline must be ( and always is) non-negative.

Each LP model must have three parts 1-3 as above.