Assume that two products, A and B, are manufactured on two

machines, 1 and 2.

Product A requires two hours on machine 1 and one-half hour on machine 2.

Product B requires three hours on machine 1 and one and half-hour on machine 2. There are eight hours of available capacity on machine 1 and ten hours on machine 2. Each unit of A produces a net increase in profit of $ 16, and each unit of B an incremental profit of $6.

Structural variables:

X₁ = Number of units of product A to be produced

X₂ = Number of units of product B to be produced

The objective function (or profit function) to be maximised is:

The constraints are:

After slack variables are introduced to convert the inequalities into equalities, we have:

Table 1:The Final Simplex Tableau

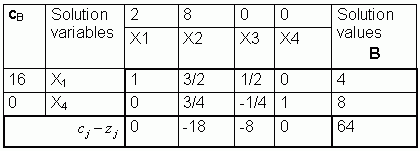
ln Table 1 all the  are 0; thus, an optimal solution has been reached. Four units of A should be produced, and this will result in a profit of $64. No other combination of products will result in as high a profit. The inclusion of eight units of x₄ in the solution indicates that machine 2 will be idle for eight hours.