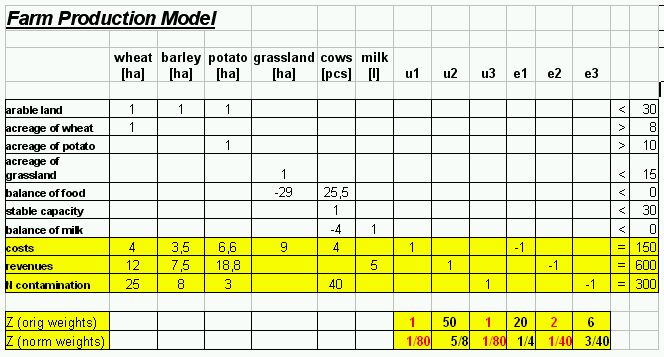
Solving these linear programming model using Linkosa software our manager obtains following optimal solution:
Let’s assume the farmers goals are: Costs $15000, revenues $60000 and N contamination 300 units. All these goals can be overachieved (with individually defined weights) or underachieved (with individually defined weights). On following Excel sheet both normalized an original weights are included, but the model is solved only with the normalized ones.

Solving these linear programming model using Linkosa
software our manager obtains following optimal solution:
| Optimal Solution of the Model FARM PRODUCTION Goal Programming Approach B | ||||||
| Min. value of the objective function Z (norm weights) | ||||||
|
31,27
|
||||||
| Structural variables | Constraints | |||||
| Name | Value | Type | Name | Value | Slack | |
| wheat [ha] |
8
|
Basic | arable land |
30
|
0
|
|
| barley [ha] |
0
|
Lower bound | acreage of wheat |
8
|
0
|
|
| potato [ha] |
22
|
Basic | acreage of potato |
10
|
-12
|
|
| grassland [ha] |
3,97
|
Basic | acreage of grassland |
15
|
11,03
|
|
| cows [pcs] |
4,52
|
Basic | balance of food |
0
|
0
|
|
| milk [l] |
18,08
|
Basic | stable capacity |
30
|
25,48
|
|
| u1 |
0
|
Lower bound | balance of milk |
0
|
0
|
|
| u2 |
0
|
Lower bound | costs |
150
|
0
|
|
| u3 |
0
|
Lower bound | revenues |
600
|
0
|
|
| e1 |
81,05
|
Basic | N contamination |
300
|
0
|
|
| e2 |
0
|
Lower bound | ||||
| e3 |
146,8
|
Basic | ||||