1.1 Decision Making

1.1.1 Decision making and problem solving
 

Our minds perform a series of information processing in order to form strategies needed to live our daily lives. This process is known as decision making.

Decision making is a process of choosing among alternative courses of action for the purpose of attaining a goal or goals. According to Herbert A. Simon, managerial decision making is synonymous with the whole process of management.

Much confusion exists between the terms decision making and problem solving. One way how to distinguish between them is to examine the phases of the decision making process. These phases are

1. intelligence
2. design
3. choice
4. implementation

Another viewpoint is that steps 1-3 constitute decision making that ends with a recommendation (step 4).

The terms decision making and problem solving we shall use interchangeably.

1.1.2. Management often requires critical decisions

Each manager has to daily make many decisions. Some of these decisions are routine, while others have great impacts on the operations of the firm for which he/she works. Some of these decisions could involve large sums of money being gained or lost, or could involve whether or not the firm accomplishes its mission and its goals. In our increasingly complex world, the tasks of decision-makers are becoming more challenging with each passing day. The decision-maker must respond quickly to events that seem to take place at an ever-increasing pace. In addition, a decision-maker must incorporate a sometimes-bewildering array of choices and consequences into his or her decision. Routine decisions are often made quickly, perhaps unconsciously without need for detail process of consideration. However, for complex, critical or important managerial decisions it is necessary to take time to decide systematically. Management requires making critical decisions that cannot and must not be wrong or fail. One must trust one's judgement and accept responsibility.

1.1.3 Decision making and Management Science

One of the greatest scientific approaches to decision making process is relatively new science: Management Science.

The field of Management Science (MS), known also as Operations Research (OR), started with the publication of The Principles of Scientific Management in 1911 by Frederick W. Taylor. It has been providing assistance to managers in developing the expertise and tools necessary to understand the decision problems, put them in analytical terms and then solve them. The OR/MS analysts are, e.g., "chiefs of stuff for president", "advisors", "R&D modellers" "systems analysts", etc.

Applied Management Science is the science of solving business problems. The major reason that MS/OR has evolved as quickly as it has is due to the evolution in computing power.

1.1.4 Decision making and modelling process

Decisions are the heart of success and at time there are critical moments when they can be difficult, perplexing and nerve-wracking. This module provides help and guidance for making good strategic decisions, which are effective, by using an efficient, effective, and systematic decision-making process. This structured and well-focused approach to decision making is achieved by the modelling process which helps in reflecting on the decisions before taking any actions.

The foundation of making good decisions is built on philosophy of knowledge, science and logic, and above all creativity.

1.1.5 Components of decision process

Almost all decision problems have environments with similar components as follow:

• The decision-maker.
• The team of analysts who models the problem in order to help the decision maker.
• Controllable factors and uncontrollable factors.
• The possible outcomes of the decision.
• The environment/structural constraints.
• Deterministic or probabilistic environment.
• Dynamic interactions among these components.

After recognizing this no-nonsense classification of decision making components, then the Management Science/Operation Research (OR/MS) analyst performs the following the sequence with some possible feedback loops between its steps:

1. Understanding the Problem: It is critical for a good decision making to understand clearly the problem, the objective, and constraints involved.
2. Constructing an Analytical Model: This step involves the "translation" of the problem into precise mathematical language in order to make calculation and comparison of the outcomes under different scenarios possible.
3. Finding a good Solution: Important here is to choose the proper solving technique, depending on whether the specific characteristics of the model. After the model is solved, validation of the obtained results must be done in order to avoid unrealistic solution.
4. Communicating the Results with the Decision-Maker: The results obtained by the OR/MS analyst have to be properly communicated to the decision-maker. This is the "sale" part. If the decision-maker does not buy the OR/MS analyst recommendations, he/she will not implement any of them.

Since the strategic solution to any problem involves making certain assumptions, it is necessary to determine the extent to which the strategic solution changes when the assumptions change. You will learn this by performing the "what-if" scenarios and the necessary sensitivity analysis.

Gathering reliable information at the right time is a component of good decisions. It is helpful to understand the nature of the problem by asking "who?", "what?", "why?", "when", "where" and "how?".

Preparation for management, whether it is related to technology, business, production, or services, requires knowledge of tools, which can aid in the determination of feasible, optimal policies.

1.1.8 Decision support systems

In addition to skills related to communication and qualitative reasoning, enterprises wishing to remain competitively viable in the future, need decision support systems (DSS) to help them understand the complex interactions between all components of a given given organisation's system, both internal and external situations.

A DSS is an interactive flexible and adaptable computer oriented system that utilisses decision rules, models and model base coupled with a comprehensive database and the decision maker´s own insight, leading to specific, implementable decisions in solving problems that would not be amenable to management science optimisation models per se. Thus, a DSS support complex decision making and increase their effectiveness.

The most important components of each DSS are:

1. Data management.
2. Model management.
3. Communication dialog subsystem.

Management Science can help reduce or eliminate the fear of making wrong decisions by providing help with decision making process. In fact, management science's goal is to eliminate decidophobia. This is accomplished through the phased processes of management science that dissect the components of the decision into workable elements and allow one to proceed to the decision making stage with sound knowledge to base one's choice. However, if you choose not to use management science, there are plenty of ways to avoid making decisions.

1.1.10 The main aim of the module

As the title of the module tells, this course is an applied one which means it is concrete not abstract or "knowledge for the sake of knowledge". This course changes your life for better. The aim of this module is to make you a better decision maker by learning the decision making process:

1. What is the goal you wish to achieve? Select the goal that satisfies your "values". Everyone has a system of values by which one lives one's life. The values must be expressed in numerical and measurable scale. This is needed in order to find the ranks among values.
2. Find out the set of possible actions you can take and then gather reliable information about each one of them. The more alternatives you develop the better decision you may make.

• A recognition of a need: A dissatisfaction within oneself--a felt void or need.
• A decision to change-- to fill the void or need.
• A conscious dedication to implement the decision.

It is this approach to decision making that makes the business into being successful. But it is important to note that such a process does not come easily. Again, this process is of a three-fold origin that encapsulates doctrines of computer integration, mathematical scaling and modelling and finally re-entering new data transformations that will occur as time tics onward. This is the complex analysis that will deduct our thinking in this regard.

1.2 How to Make Serious Decision?

1.2.1 There are many possible methods - serious and non-serious which can support decision making process
 

There are many strange methods of human choice. A sample of the most popular methods follow (according to Arsham):

1. Recourse to someone or even something else:

Examples are astrology (not astronomy which is a science), palm readings, looking up at stars, dialling 1-900 psychic friends, reflexology (your feet know), iridology (your eyes know), telepathy, telekinesis, the aura, crystals, dreams, colors, Feng Shui, numerology, fortune-tellers, etc. All these -logy, which is Greek for "word", are idols for worshipping. This even includes all the ideologies presented throughout history.
 
2. Do not think about it:

As Henri Poincare said, "Doubt everything or believe everything: these are two equally convenient strategies. With either, we dispense with the need to think for ourselves."
 
3. Do anchoring:

Give disproportion weight to some information instead of waiting, as long as possible, to have all the information.
 
4. Sunk-cost conscious:

Repeat the same decision because "you have invested so much in this approach (or your current job) that you cannot abandon it or make another decision (or look for a better position)."
 
5. Failure to reflect on the problem:

Reflection before action is often resisted by some managers because for them reflection takes too much time, it requires too much work, and they do not know much about decision problem/opportunity.
 
6. Look for confirming-evidence:

Seek out the information to support an existing pre-selection and discount opposing ones.
 
7. Pray for it:

Whatever we pray for, we pray for a miracle. Every prayer reduces itself to this: "Great God, grant that twice two be not four".
 
8. Be over-confident:

This makes you optimistic and then take a high risk decision.
 
9. Be too prudent:

Be over curious long enough to delay the decision. If you are too careful, you are so occupied in being careful that you are sure to stumble over what you are going to decide.
 
10. Pass the buck:

Pass off responsibility of making the decision to someone else. Do not make decisions by yourself. Bring in someone to blame if things go wrong. For example, for life's problems one may marry. Remember that it takes two to tango.
 
11. Succumb to failure:

Believe that the choices you will make are predestined and you are bound to fail (one gets used to failure) versus the result of hard work and thought.
 
12. Set up a committee:

To make decisions, try to set up a committee not necessarily consisting of experts. So if everything goes well, every member is proud of such a decision. But if everything goes wrong, nobody is responsible. Every member would say, "It was not I; it was the committee's decision. You see, we couldn't agree, therefore we voted". Put a face to a faceless group, call it "the committee." The committee's members, who are wishing that just to vote in "either/or" fashion are those who are not ableto contribute to the decision making process, therefore shouldn't be trusted with an important decision. A group decision support system could be a technologically advanced version of this strategy. Of course setting up committee could be done correctly with the proper experts but one person should be the decision maker and responsible for the decision.
 
13. False decentralisation:

Decentralisation is could take place when an authoritative manager delegates accountability to a new "director of…" for every new decision-making problem, but not delegating any authority.
 
14. Failure to define the problem:

This certainly lends to a wrong solution. Not knowing the problem, any solution is wrong. Knowing the problem then, your solution might be good.
 
15. Failure to understand the problem:

This is caused, among others, by subjectivity, irrational analysis, lateness or procrastination, lack of sensitivity, and lack of focus.
 
16. Complexity is confusing to the decision maker:

Simplify and even change the problem to something which you have a strategic solution for (e.g. this is committed by many OR/MS analysts when they change the model to fit their strategic solution algorithm).
 
17. Rationalisation to limit the course of actions:

This strategy is very popular. Stack the cards to make one alternative clearly right and remove all risk.
 
18. Information:

Information gathered is not valid. Decisions are often made first and information sought to support the solution, or much information gathered is irrelevant to the decision making.
 
19. Decision is only symbolic:

One will fight hard for a policy and then indifferent to its implementation.
 
20. The Decision maker has obligations:

Sometimes decision makers act against integrity to meet some critical personal obligations.
 
21. Best of all, decline responsibility:

Stagnate or do nothing is another possible one. Some people do this in belief that the right strategic solution will eventually become obvious. Decline all responsibility, or still better, do nothing; i.e., status quoism. However, "not to decide is to decide". A business leader makes decisions. Whether they are right or wrong, they get made, and they are clear. A weak leader procrastinates and gives false signals, leaving subordinates to charge off in different directions. One must trust ones gut felling and block for scapegoats or to substitute responsibility unconditional.
 
22. Post-decision anxieties:

The more highly desirable the alternatives that must be rejected and the faster the decision must be made, the greater are these anxieties (also known as cognitive dissonance). Most people accentuate the positive in their decision and deny or ignore the positive aspect of the rejected alternatives.
 
23. Solving a problem by creating a new one:

Often, because of deep frustrations in facing a difficult problem, one may unfortunately solve it by creating a bigger problem. This strategy tries to get rid of a present problem with unfortunate by-product of forming a new problem. As an example, not willing to face the difficulties of the problem courageously, one desperately uses alcohol as a tranquiliser. However, after a while he or she realises that while alcohol kills germs, it certainly removes the personal dignity and everything else with it.
 
24. Decision Problems or Decision Opportunities:

Decisions are an inevitable part of human activities. With a right attitude, in some situations decision-maker must view the problems as taking the opportunities rather than solving problems. For example, suppose you receive a serious complain letter from a dissatisfied customer. You may turn this problem into an opportunity by finding more on what is wrong with the product/service, learning from the customer experience in order to improve the quality of your product/service.
 
25. Pros-Cons-Interesting implications method:

Most of your decisions can be made using your past experiences, a little thinking and common sense. But when you encounter problems where one wrong decision could have adverse long-term effects and might lead to severe mistakes and considerable failures. Sometimes small decisions turn out to be very important in consequence, examples are in abounded in traffic accidents.
 
26. Subjective and Objective Decision-Making:

Your decisions might be categorised as into two groups with some possible overlaps in some cases. One is subjective which are private, such as how you want to live your life, or decide on something just because "It feels good". In subjective decisions you might also consider your strengths, weakness, opportunities and threats. The other group of decisions is objective, purely unemotional decision-makings, which are public, which need to "Stepping outside yourself" so that you discount your emotions. For examples, a CIO deciding for the company must ask among other questions "Can I convince the share-holders?" This group of decision making involves responsibility, which requires rational, defensible and accountable decision. Therefore, the first group consists of private decisions which might involves emotion, and the second almost entirely rational decision making. However, the really hard decisions involve a combination of both. The difficulty might arise from the fact that emotions and rational thinking are on two different sides of human brain, and in difficult decisions one must be able to use both sides simultaneously.

1.2.2 The goals and preferences influence decision making

Decision-making involves a series of steps. The process begins with the formation of goals and proceeds to the identification of problems and alternative courses of action. It does not end until well after the decision or choice is actually made and the post decision anxieties have been experience. Decision making, however, is one management function that is important at all points in the process of management.

A decision-maker must first decide about his/her values and to set goals to insure fruitful decision making process. Before taking any course of action one must discover/create a set of alternative course of actions and gathers information about each. Having gathered the information with which to make a decision, one must apply information for each course of action to predict the outcomes of each possible making a decision for implementation. Keep in mind that each decision is influenced by decision maker´s attitudes.

1.2.3 Decision making and inter-team communication

OR/MS is a systems approach to problem solving in that it considers the context of the problem as important as the problem itself. It utilises a team approach by capitalising on the talent of an OR/MS analyst to assess, co-ordinate, and incorporate knowledge relevant to solving a certain decision problem from experts in other fields, (known also as think-tank approach). The difficulties in clear communication among the team members in any OR/MS project can increase with the size of the team.

A decision is a reasoned choice among alternatives. Making a decision is part of the broader subject of problem solving. Although the management science approach can be used to construct a mathematical model, it is useless if the result is too complex to be communicated to the decision maker. The end result is a product that is incomprehensible to the decision maker. To avoid such an outcome, the analysis should be done in stages. You must overcome the communication barriers.

Depending on the audience of the report, the mathematical model may or may not be included. It is the task of the management science team to write a report that is understandable by all that will read it.

1.3 Operations Research and Management Science (OR/MS)

1.3.1 The complexity of the global world needs scientific approach

The mass production available through the application of new technology and the concomitant penetration of massive markets for the goods produced, enterprise possessing sufficient capital organised men and machines create the factory system. Today there are many large man-made systems besides factories, such as hospitals, airports, and telecommunication systems. Larger companies employ thousands of workers, deal in billions of dollars, manufacture hundreds of products, and service a multitude of markets. The service industries, including banks, hospitals, insurance companies, consulting firms, and governments, are faced with operational complexities similar to those noted for the manufacturing industry.

The complexity of today's business operations, aggressive competition, and government controls have made the job of the manager increasingly difficult. It is no longer possible for one individual to be aware of the details of every characteristic of the firm or to make all decisions regarding its operation. Even within a manager's relatively small span of control the factors affecting his decisions are often so numerous and their effects so pervasive that standard ways of making decisions are no longer acceptable. As a result, effective decision making often requires the availability of information analysed and summarised in a timely fashion.

1.3.2 Management Science as a new science

The large system the more application of scientific techniques science have to be involved into decision making process. Scientific approach to decision making is a fundamental characteristic of modern industry and society. Why we must learn decision-making process? Here are a few motivating reasons:

• Organisations are becoming more complex.
• Environments are changing so rapidly that past practice are no longer adequate.
• The cost of making bad decision have increased.

Operations Research (OR) known also as Management Science (MS) is the science of making decisions. What is in the name Management Science? To manage means to be in control and being able to predict what is not controllable. Science is a continuing search; it is a continuing generation of theories, models, concepts, and categories. Therefore, Management Science is the science for managing which almost always involves decision-making.

1.3.3 Management Science and related names

This analytical approach is known by several different names:

1. Operations Research (a US-ism)
2. Operational Research (a UK-ism)
3. Decision Sciences
4. Systems Science
5. Mathematical Modelling
6. Industrial Engineering
7. Critical Systems Thinking
8. Systems Analysis and Design

1.3.4 Model approach

The typical OR/MS approach is to build a model for the problem being studied. Such a model is often (but not always) mathematical. Practical problems are often unstructured and the definition and clarification of problems, as well as the building of models, is an important part of the OR/MS methodology. Most people discover that the understanding created by building a model is a very valuable part of an OR/MS project. Once a model is built, algorithms often have to be used to solve it. An algorithm is a series of steps that will accomplish a certain task. The study, understanding, and invention of such algorithms is also an important part of OR/MS modelling for decision-making. The decision maker might incorporate some other perspectives of the problem such as cultural, psychological, etc., into the management scientist's recommendations. Finally, communicative and political skills are needed in implementing the results of an OR/MS model in a real-life situation. OR/MS models are aimed at assisting the decision-maker in his/her decision-making process.

1.3.5 System approach

OR/MS modelling process is more than a set of analytical methods. OR/MS models are aimed at assisting the decision-maker in his/her decision-making process. A fundamental part of OR/MS modelling is the "systems approach" to problem solving. This approach instructs that the context of organisational problems is as important as the stated problem. Defining a problem, collecting data, consulting with people involved in the solution, and implementing change are all aspects of the OR/MS education and training. As it is easier to make plans than to carry them out, models that are not to be implemented are ones that were not drawn up correctly and taken seriously from the start.

1.3.6 OR/MS modelling process

OR/MS modelling process helps to improve operations in business and government through the use of scientific methods and the development of specialised techniques. Operations Research is not "research"; it is the process cycle of re-searching for an optimal (or desirable) strategic solution to the existing decision problem/situation. OR/MS modelling process provides systematic and general approaches to problem solving for decision making, regardless of the nature of the system, product, or service. The approaches and tools used in OR/MS models are based on one or more of the following analytical methods, simulation, and qualitative or logical reasoning. Many of these tools and approaches depend on computer-based methodologies for implementation.

OR/MS modelling process is the application of scientific methods to complex organisational decision problems/opportunities. OR/MS models are aimed at assisting the decision-maker in his/her decision-making process. This modelling process is now widely used in the manufacturing industry, least cost distribution of goods, and finance functions as well as in service industries, and the health and education sectors. Improvement of an existing system and good designs for new systems are the aims of OR/MS.

OR/MS modelling process is one of the greatest innovative decision making tools of the twentieth century. OR/MS has been developed since the end of the World War II (see history of MS/OR).

1.3.7 The definition of MS/OR

Many definitions of OR/MS have been offered, as well as many arguments as to why it cannot be defined. The following definitions provide a useful basis for an initial understanding of the nature of OR/MS:

1. A scientific method of providing executive management with a quantitative base for decisions regarding operations under their control (Mores-Kimball 1943).
2. The application of the scientific method by inter-disciplinary teams to problems involving the control of organised (man-machine) systems so as to provide solutions which best serve the purpose of the organisation as a whole (Ackoff- Sasieni 1968).
3. Scientific approach to problem solving for executive management (Wagner 1969).
4. Optimal decision making in, and modelling of, deterministic and probabilistic systems that originate from real life. These applications, which occur in government, business, engineering, economics, and the natural and social sciences, are largely characterised by the need to allocate limited resources. In these situations, considerable insight can be obtained from scientific analysis, such as that provided by OR/MS (Hiller-Lieberman 1974).
5. A branch of applied mathematics wherein the application is to the decision making process (Gross 1979).

In examining these definitions, it should be noted that neither the old and well-established scientific discipline nor science itself has ever been defined in a way that is acceptable to most practitioners.

1.3.8 The phases of application of OR/MS

OR/MS is the scientific (mostly mathematical) method of decision-making. In most discussions of the scientific method, the following eight stages are cited as being essential:

1. Perceiving the need
2. Formulating the problem
3. Constructing a model
4. Deriving a solution
5. Validation and verification
6. Establishing controls
7. Implementation and recommendation
8. Evaluation of the results

1.3.9 The standard applications

An important consequence of the application of OR/MS to a wide variety of problems is that a small set of problem types have been identified which account for most problems. Because of the frequent recurrence of these problems, prototype techniques have been developed for modelling them and for deriving solutions from these models. Prototype applications include:

1. Forecasting: Using time series analysis to answer typical questions such as: How big will demand for products be? What are the sales patterns? How will this affect profits?
2. Finance & Investment: How much capital do we need? Where can we get this? How much will it cost?
3. Manpower planning & Assignment: How many employees do we need? What skills should they have? How long will they stay with us?
4. Sequencing & Scheduling: What job is most important? In what order should we do jobs?
5. Location, Allocation, Distribution & Transportation: Where is the best location for an operation? How big should facilities be? What resources are needed? Are there shortages? How can we set priorities?
6. Reliability & Replacement Policy: How well is equipment working? How reliable is it? When should we replace it?
7. Inventory Control and Stockout: How much stock should we hold? When do we order more? How much should we order?
8. Cost-Benefit Rules: Given the decision maker's assessment of costs and benefits, which choice should be recommended.
9. Project planning and control: How long will a project take? What activities are most important? How should resources be used?
10. Queuing and Congestion: How long are queues? How many servers should we use? What service level are we giving?

1.3.10 Career opportunities for specialists in MS/OR

Completion of the course of OR/MS enables graduates to find employment as OR/MS analysts, academicians or managers. It is a fact that education and work in OR/MS can lead to the executive suite where decisions are made. Career opportunities in the following areas of business are excellent:

Manufacturing, Insurance, Planning, Systems analysis, Marketing, Budgeting, Finance, Program evaluation, Banking, Services.

OR/MS profession should be particularly considered by persons who are attracted to the use of mathematics, statistics, and other branches of science, in general, for solving decision making problems of practical significance.

Some individuals believe that OR/MS is viewed as a "young person's" profession. Given the fact that analytical modelling is at the heart of OR/MS activity, such an assertion might be relevant. This belief originally came from the mathematical community.

1.3.11 OR/MS as Systems Engineering

Today the word "Engineering" has a broader meaning and scope than merely dealing with physical engines. The word engineering in phrases such as re-engineering business activities has much wider scope. For example, economists like to think of themselves as something like 'engineers' trying to keep the 'train' of state on track. Building upon foundations in mathematics, statistics, operations research, and economics, Systems Engineering involves the design, control, and management of complex systems arising in manufacturing, transportation, telecommunications, and the environment. By considering the system as a whole, rather than as individual components, Systems Sciences provide direction as to the optimal design of the business systems, as well as their on-going operations and maintenance.

Systems engineering exists as a discipline because the complexity of large scale systems tends to defy effective design of the whole. The core of the discipline focuses on certain areas of mathematics and methodology, rather than on particular physical sciences, as is typical of other engineering specialities. Systems engineers learn to model, simulate, optimise, integrate, and evaluate systems. They participate in group projects in such systems application areas as environmental control, telecommunications, transportation, project/construction management, and manufacturing.

1.3.12 OR/MS as Industrial Engineering

Industrial Engineers design systems to enable people and society to improve productivity, efficiency, effectiveness, and quality of the work environment. All engineers work at planning, designing, implementing, and controlling the systems that represent the way people use technology. The systems that are the subject of Industrial Engineering design are broad and are characterised by a need to integrate both the physical and decision-making capabilities of humans together with all other aspects of the system design. The following show the range of problems:

1. The design of a work method and work station.
2. The design of a factory layout and methods of controlling the flow of materials on the factory floor.
3. The design of an overall corporate plan involving materials procurement, production, inventory and distribution.

Human behaviour and capabilities are key elements in the systems with which Industrial Engineers work. In designing the layout of a production line for an automobile manufacturer, the checkout counter for a supermarket, the organisation of office work flow for a bank, a materials handling system, or a steel plant, the engineer must consider physical requirements, cost parameters, and the physiological and behavioural performance of the human operators. The Industrial Engineer has a dual role to extend human capability to operate, manage and control the overall production system and to ensure the safety and well being of those working in the system.

Design and development of these systems require the unique background of the Industrial Engineer. The process of engineering always starts with measurement. Where other engineers might measure temperatures, pressures, or wind loads, the Industrial Engineer measures the time of a work cycle, dollar values of expenditures, rates of machine failures, or demand processes for finished goods. Usually the mathematical analysis must take into account risk and uncertainty to a larger extent than in other engineering fields. Computer simulation and optimisation are often required. The concepts and techniques found in Industrial Engineering are to assist you in developing the skills that meet the specific challenges of systems which involve managerial activities.

1.3.13 OR/MS as Management Information Systems

There is much overlap between the OR/MS and Information Systems fields. Many business operations require intensive knowledge of computing and information systems. Similarly, management of computing and information facilities often require a deep understanding of issues such as scheduling, replacement strategy, and policies on the development and adaptation of new technology.

The business world is becoming more computer and information intensive; therefore, specialists in OR/MS and Information Systems combine a background in OR/MS modelling process and a good knowledge of current computing technologies. They design and manage computerised systems that control the production and distribution of a firm's goods and services. Career opportunities exist in most industries and government organisations in the areas of systems analysis and design.

1.3.14 OR/MS as Production and Operations Management

Operations Management is the functional area of business that is concerned with the production of goods and services. In conjunction with other functional areas, it also deals with the management of resources (inputs) and the distribution of finished goods and services to customers (outputs).

Operations refers to the production of goods and services -- the set of value-added activities that transforms inputs into outputs.

Operations Management is concerned with management of the production and distribution of the goods and services of a firm or government organisation. Issues in the management of operations include: Forecasting of the demand for the organisation's products and/or services; Development of efficient manufacturing processes; Inventory planning and control; Work force scheduling; and Design and management of distribution and transportation networks.

The study of Operations Management embraces the disciplines of Operations Research, Statistics, and Computing and Information Systems. This field is a blend of field studies and the use of computerised models to analyse and simulate the operation of real systems.

Operations are at the heart of most organisations, and opportunities are found in the area of forecasting, inventory management, the design of production facilities, work force scheduling, and the location and layout of distribution networks. Specialisation in Operations Management is particularly useful when combined with the study of another functional area of business such as marketing, finance, or management information systems.

1.3.15 Modelling is basic technique used in MS/OR

OR/MS approach to decision making process is mostly through mathematical models. The use of mathematical modelling spreads to the public and private sector and has grown rapidly since the availability of PC.

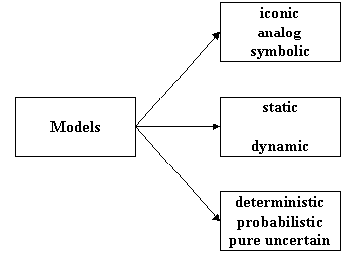
Models are categorised according to their distinctiveness such as kind, evolutionary in time, as well as accessibility of records:

Models can be

Iconic - they are static in nature

Analog - they act like reality but often not appear like reality

While system model may take many forms, it usually includes the logical relationships between the variables affecting system performance and some measure (or measures) of system performance. These relationships are frequently expressed in a mathematical form. By altering values of the values of the variables in these relationships, the manager or analyst can determine the effect of the variety of the conditions on the operational effectiveness of the system described by the model. Mathematical and computer models are known as symbolic models.

1.3.16 General classification of models

By analysing we process information to represent reality. The result is a "model". Therefore, a model is a re-presentation of reality. To achieve an accurate model one must use a mathematical modelling process cycle. Mathematics was invented by humans in an attempt to define life in their own terms.

A decision-maker must identify which type of model best suits the decision problem. Although OR/MS mostly concentrates on mathematical models the other model types are also prevalence in practice.

Models can be classified according to their characteristics such as types, evolution in time, and availability of information, as shown, for example, in the following figure.

A Classification of Models

Compared with mechanical models, mathematical models facilitate experimentation because all dependent variables, independent variables, constants, and parameters are explicitly related through the language of mathematics. The decision-maker can test the effects of different decision alternatives, constants, and parameter values on the dependant variables much more easily than with any other type of model. Further more, mathematical models can represent many complex problems efficiently and concisely and, in many cases, provide the cheapest way to analyze these problems. It is for these reasons that we address the various mathematical models and solution techniques most often used in practice.

All decision-making models can be classified as either Deterministic Models or Probabilistic Models. This depends largely on how influential the uncontrollable factors are in determining the outcome of a decision. Unlike deterministic models, the probabilistic models are viewed with the awareness of theory of games and expected outcome. The centre of interest moves from the deterministic to stochastic using statistical estimations and predictions. Unlike deterministic models where good decision is judged my its outcome alone, in probabilistic models the decision maker is concerned with both the outcome value and the amount of risk each decision carries. We will cover both deterministic and probabilistic decision making process.

1.3.17 Descriptive and normative analytical models

Mathematical and computer symbolic models are described by means of analytical mathematical means: systems of functions (equalities and inequalities). That is why we can call them analytical models and decision making based on these models is called analytical decision making.

The analytical decision making process is an assessment based on the choice of alternatives. That is, choosing the alternative that fits the need of the person or organisation. In order to provide solutions through modelling one must obtain the facts, eliminate things that are not relative, understand the real decision problem/opportunity.

MS/OR approach to decision making uses two types of analytical models:

1. Descriptive models:

1. Normative models

- get the highest level (maximum) of goal from given set of resources

- find the alternative with the lowest cost (minium, minimatisation of resources) that will fulfill a required level of goals

- find the alternative with the highest ratio of goal attainment to cost, or in other words, maximise productivity

Mathematical modelling can claim to be the most original creation of mankind. The originality of this modelling lies in the fact that in model building connections between things are exhibited which, apart from the agency of human reason, are extremely unobvious. Thus the ideas, now in the minds of modellers, lie very remote from any notions that can be immediately derived by perception through the senses; unless it is perception stimulated and guided by an antecedent modelling process.

1.3.18 More about mathematical models

A mathematical model is an equation, inequality, or system of equations or inequalities, which represents certain aspects of the physical system modelled. Models of this type are used extensively in the physical sciences, engineering, business, and economics.

A model offers the analyst a tool which he can manipulate in his analysis of the system under study, without disturbing the system itself. For example, suppose that a mathematical model has been developed to predict annual sales as a function of unit selling price. If the production cost per unit is known, total annual profit for any given selling price can easily be calculated. To determine the selling price which will yield the maximum total profit, various values for selling price can be introduced into the model one at a time, the sales resulting noted, and the total profit per year computed for each value of selling price examined. By trial and error the analyst could determine the selling price which will maximise total annual profit.

Ideally, if the mathematical model is a valid representation of the performance of the system, by the application of the appropriate analytical techniques the solution obtained from the model should also be the solution to the system problem. Thus the effectiveness of the results of the application of any operational technique is largely a function of the degree to which the model represents the system studied. To define those conditions which will lead to the solution of a systems problem, the analyst must first identify a criterion by which the performance of the system may be measured. This criterion is often referred to as the measure of the system performance or the measure of effectiveness. In business applications the measure of effectiveness is often either cost or profit, while this measure is more often defined in terms of a benefit-to-cost ratio in governmental applications.

The mathematical (i.e., analytical) model which describes the behaviour of the measure of effectiveness is called the objective function.

1.3.19 Optimisation in MS/OR

Mankind has long sought, or professed to seek, better ways to carry out the daily tasks of life. Throughout human history the long quest for more effective sources of food in the beginning and then later materials, power, and mastery of the physical environment. Relatively late in human history, however, certain kinds of general questions began to be formulated quantitatively, first in words, and later in symbolic notations. One pervasive aspect of these general questions was a seeking after the "best" or "optimum." Most of the time managers seek merely to obtain some improvement in the level of performance, i.e., a "goal-seeking" problem. It should be emphasised that these words do not usually have precise meanings.

Massive efforts have been made to describe complex human and social situations. To have meaning it should be written down in a mathematical expression containing one or more variables, the value of which is to be determined. The question that is then asked, in general terms, is what values should these variables have so that the mathematical expression has the greatest possible numerical value (maximisation) or the least possible numerical value (minimisation). This general process of maximising or minimising is referred to as optimisation.

Early we classified all decision-making problems into two categories: deterministic and probabilistic decision models. In deterministic models your good decisions bring about good outcomes. You get that what you expect, therefore the outcome is deterministic (i.e., risk-free). This depends largely on how influential the uncontrollable factors are in determining the outcome of a decision and how much information the decision maker has in predicting the these factors.

Those who manage and control systems of men and equipment face the continuing problem of improving (e.g., optimising) system performance. The problem may be one of reducing the cost of operation while maintaining an acceptable level of service, profit of current operations, providing a higher level of service without increasing cost, maintaining a profitable operation while meeting imposed government regulations, or "improving" one aspect of product quality without reducing quality in another. To identify methods for improvement of system operation one must construct a synthetic representation, or model, of the physical system, which could be used to describe the effect of a variety of proposed solutions.

1.3.20 Model and reality

A model is a representation of reality from the modeller's perspective. Therefore, you must develop a multi-perspective model of the problem on hand to understand the problem.

The analytical results obtained from an analytic model must always be tempered with experienced judgment, since there usually exist factors that cannot be accounted for in the model. However, an analysis of the system through the use of a reasonable model usually provides valuable input to managerial decisions.

Modelling is a structured consecutive-focused-thinking process for understanding reality for utilitarian purposes.

A mental model is a representation of your thoughts about reality. Therefore, it is an objectification of reality, which in turn means the subjective begetting of the reality. Mathematical models employ symbols and notations, including numbers. Thus, there are three distinct concepts involved into modelling process:

1. The reality
2. The mental model
3. Reality representation by means of the model

1.3.21 Model as a learning activity

The process of observing the system is a learning activity. Therefore, this is a tripartite concept, namely, Thinker-and-Learning-and-System. There are a variety of orders in which the three concepts could be arranged. For example, "systems for learning", which is mainly our educational institutions.

1.3.22 Modelling is multi-discipline process

Modelling is the science of making optimal judgment that require a combination of many disciplines. Since decision making is a central human activity. Therefore, OR/MS encompasses many disciplines of study. OR/MS models are aimed at understanding the problem and assisting the decision-maker in his/her decision-making process. Models explain the problems and provide solutions.

1.3.23 Controllable and non-controllable variables

Since a model of a system is a re-presentation of the system that contains those elements that affect the objective of our decision, it is important to identify the most important input elements.

The desired output usually determines the controllable inputs.

The input into a system can be classified either as controllable or uncontrollable inputs, as the figure below illustrates. Time-horizons for the modelling review must be selected that are short enough so that the uncontrollable inputs (or probabilistic knowledge of them) will not change significantly. The output is often called the performance measure of the system. Where performance is measured, performance improves. Where performance is measured and reported, the rate of improvement accelerates. The following Figure depicts the OR/MS structured decision making process approach. Remember that, when structures and systems are aligned, they facilitate empowerment. When they aren't, they work against it.

Structured Decision Making Process and Its Components according to H. Arsham:
Analysis, Design, and Control

1.3.24 What-if analysis through the model

OR/MS models are aimed at assisting the decision-maker in his/her decision-making process. In the decision making modelling process we investigate the effect of presenting different decisions retrospectively; that is, "as if" the decision has already been made under different course of actions. That is why the sequence of steps in the modelling process must be considered in reverse order. For example, the output (which is the result of our action) must be considered first.

1.3.25 The components of the modelling process

It is helpful to understand the nature of the problem by asking "who?" "What?" "Why? " "Where? " "When?". Finally breaking them into three groups: uncontrollable, controllable (set of all your possible choices), and the parameters that defines the problem. As indicated in the above activity chart, the decision making process has the following components:

1. Performance measure: Provides the desirable level of outcome (objective of your decision). Objective is important in identifying the problem. The major task for the decision-maker is the solution to the problem of "values" among different objectives, and the selection of a single objective that has the "highest value". Then if needed, all other objectives should be included in the set of constraints to be satisfied.
2. Uncontrollable inputs: Come from the decision maker's environment. Uncontrollable inputs often create the problem and constrain the actions.
3. Parameters: Parameters are the constant elements that do change during the time horizon of the decision review. These are the factors partially defining the problem.
4. Controllable Inputs: Controllable inputs are the collection of all possible courses of action you might take.
5. Interactions Among These Components: These are logical, mathematical functions representing the cause-and-effect relationships among inputs, parameters, and the outcome. There are also set of constraints which apply to each of these. Therefore, they do not need to be treated separately.
6. Actions: Action is the ultimate decision and is the best course of strategy to achieve the desirable goal. Decision making involves the selection of a course of action (means) in the pursuit of one's objective (ends). The way that our course of action affects the outcome of a decision depends on how the inputs and parameter of the problem are interrelated and how they relate to the outcome. Functionality is the most important type of relationship involved in the decision making process interactions. When the outcome of a decision depends on our course of action, we change one or more aspects of the problematic situation with the intention of bringing about a desirable change in some other aspect of it. We succeed if we have knowledge about the interaction among the components of the problem.
7. Controlling the Problem: Few problems in life, once solved, stay that way. Changing conditions tend to un-solve problems that previously had been solved, and their solutions create new problems. One must identify and anticipate these new problems.

A mathematical (i.e., analytical) model is the one whose relationships are expressed in the rigorous language of mathematics. In this way, a mathematical model is abstract because one cannot visualise the system it is supposed to portray by merely looking at it.

Components of analytical modelling process:

1. Classification of knowledge:

knowledge about objects, events, processes, relations
 
2. Types of comprehension:

understand, interpret, relate, select, recall, compare
 
3. Types of analysis:

relate, compare, interpolate, extrapolate, generalise, specify
 
4. Results of model evaluations:

accept, reject, possible, irrelevant

1.3.27 The process cycle of the analytical modelling

Decisions deserve appropriate time. As a decision scientist, you want the opportunity to see a decision unfold, revealing opportunities for study and assessment. The general procedure that can be used in the process cycle of decision making contains the following similar steps:

1. Understand the problem.
2. Description.
3. Prescription.
4. Post prescription.
5. Feedback and control.
6. Validation.
7. Verification.

 

 

1. Understand the problem

A model may prove to be inadequate even when it attempts to capture the appropriate elements of reality if it does so in a distorted or biased manner. An equation predicting monthly sales volume may be exactly what the sales manager is looking for but could lead to serious losses if it consistently yields estimates of sales which are high. A thermometer which reads too high (or low) would be of little use in medical diagnosis. Hence a useful model is one which captures the proper elements of reality with acceptable accuracy.

2. Description of the Problem

You must also use the system approach when describing your decision problem. A good model is both inclusive (i.e., it includes what belongs to the problem) and exclusive (i.e., shaved-off what does not belong to the problem). To use and old cliché, it should not be hard to see the forest because of all the trees.

Be concrete rather than abstract. Identify the factors influencing your decision, and find out what is and what is not under your control. Unless the problem is clearly formulated by the management scientist and accepted by the owner of the problem as the "same," it is likely that the strategic solution will be rejected by the owner of the problem. In some cases, a strategic solution to the existing problem may even create new problems. OR/MS modelling process will not solve a decision problem, nor is it intended to. Its main purpose is to produce insight and promote creativity to help decision makers make a "good" decision.

3. Prescription of a Solution

The decision problem is often stated by the decision maker in non-technical terms. When you think over the problem and find out what module of the software to use, you will use the software to get the solution. The strategic solution should also be presented to the decision maker in the same style of language which is understandable by the decision maker. Therefore, just do not give her/him the computer printout. You must also provide managerial interpretation of the strategic solution in some non-technical terms.

4. Post-prescription

"Everything is changing"; except this fact that "Everything is changing." Accept this fact. Therefore you must allow for revising the model as necessary. This means constantly updating the prescribed solution. This stage of problem solving is practiced in the free-based economy societies in contrast to the programmed-based economy societies where the model (i.e. the program) is taken more seriously than reality itself! The model is in the service to reality, not the other way around.

5. The Importance of Feedback and Control

The above focused and structured process is depicted as the Systems Analysis, Design, and Control stages, respectively, as shown in the following flow chart, including the validation and verification activities:

 



6. Validate the Model

During the validation the management scientist asks the question, "What does this model have to do with the real world?" Finally, as it is easier to make plans than to carry them out, models that are not to be implemented are not drawn up correctly and not taken seriously from the start. Here is a question for you: "Why does a dead fish weigh more than when it was alive?"

An excellent example is the presentation of the above question, "Why does a dead fish weigh more than when it was alive?" to members of the Royal Society. This provoked extensive and often ingenious attempted explanations; unfortunately, the critical fact that the statement was false was never considered. In our headlong rush to figure out the solution, we forget to think about the problem itself. We must carefully think about information and its validity as it presented to us.

7. Verify the Model

An effective way to learn about a good strategic decision-making process is to have a computer-supported capability that assures the user that the Systems Analysis, Design, and Control processes to make good strategic decisions, it does not matter whether the user is a novice, or an expert about his/her organisational environment.

1.3.28 More about validation of the model

The model-validation step is given the least attention by novice model builders. In this step the assumptions and the logic in the relationships are tested to see if they conform to reality. Model validation is a two-step process. The first step is two determine whether the model is internally correct in a logical sense. Even though tests for this would depend on the type of model being validated, several suggestions can be made.

1. Compute some outcomes with the model that can be verified with hand calculations when computers must be used to solve the model.
2. Run separate segments of complicated models alone so that the results can be verified.
3. Eliminate random elements from stochastic models to ease verification of essential logic.
4. Replace complex probability functions with elementary ones so that results are more easily verified.
5. Construct simple test situations that test as many combinations of circumstances in the model as feasible.

When the output is in the form of mean values, variances, proportions, or probability distributions, various statistical tests can be used to test the hypothesis that these output elements differ significantly from the actual mean values, variances, proportions, or probability distributions. However, when the model has been constructed for a problem in which there are no past data with which to compare, the model builder must rely on a thorough, logical check and a careful study of the model results for any discrepancies or unusual circumstances. This approach to model validation is used, for example, when a normative model is being validated or when a model has been built to propose a solution to a problem never before faced by the decision maker. In addition to checking the logic and studying the results, there are several questions that could help in assessing the validity of a model. These questions include: How many previously known theorems or results does the model bring to bear on the problem; How obvious is the interpretation of the model; How sensitive is the model to changes in the assumptions that characterise it?

If the model contains some previously known theorems or results, or if the model has much intuitive appeal, the model builder can be more confident in the model. However, a model whose outcomes are quite sensitive to changes in the assumptions should be studied further with regard to the nature of the assumptions made in the problem-definition step.

There could be a number of reasons why a model would fail the validation step. Sometimes the model is intractable or too complex to work with and thus cannot be adequately verified. Morris provides some suggestions for simplifying complex models.

1. Make some variables into constants
2. Eliminate some variables entirely.
3. Use linear relationships instead of non-linear relationships.
4. Add stronger assumptions and restrictions.
5. Suppress randomness.

1.3.29 Cost of modelling process consideration

Modelling can be very expensive. The more complicated the model, the greater the cost. Inputs and constraints added to existing problems create extra costs.

Cost Consideration: Model construction can be very expensive. It may not be prudent to spend $500,000 to develop a model that may return $50,000. The reason these models are expensive to build is that they can become very complicated as inputs and constraints are added. It is time consuming to identify and correctly correlate these items to a mathematical model, and this model must be a correct interpretation of a complex system. Unfortunately, this complexity fosters a wealth of things that can go wrong or be misinterpreted, and that results in the entire model not responding as a accurate mathematical representation of reality. An even worse case scenario is that the model may respond with total falseness. In this case, the results can be disastrous to the decision making process and to the firm itself. Accuracy is paramount in the problem definition as well as the mathematical expression.

As an example, the F-22 is being recognised as one of the most successful, best managed a new generation weapons system development a model for its program. However, as demand continues to fall in other defense programs served by the F-22 team, a portion of the fixed and overhead costs formerly supported by those programs automatically shifts over to the F-22. The danger is that this model program could ultimately become unaffordable because of the growing overhead and fixed cost burdens.

The amount of time it will take to complete the decision modelling process mostly determines the costs the data gathering and processing. The more data (i.e., information) that is collected the more it costs. Of course, the more relevant data collected closer the model is in representing the reality. Some companies are satisfied with "ball park" results to save on the cost and get the results quicker. The "ball park" results use less data and more assumptions (ass-u-&-me) which may not be accurate.

1.3.30 Difficulties of Analytical Modelling Process

Most real world problems cannot be formulated adequately as mathematical models. Since the real world problems are usually of large-scale they must be stated in a very rigid algebraic form in order to be solved by computerised algorithms. The modeller must analyse the characteristics of problem situations a legitimate in order to formulate and represent the problem as a valid analytical model. Almost all-real world problems are characterised as having the following difficulties:

1. Many conflicting "fuzzy" goals (objectives).
2. A lack of specificity as to what the decision variables (and hence those variables subject to control) and the fixed inputs (parameters) are.
3. Uncertainty as to the bounds or restrictions on the decision variables and their functions.
4. A lack of knowledge of cause-effect relationships.
5. Stochastic (probabilities) elements.
6. An underlying dynamic character tat causes the goals, restrictions, and cause-effect relationships to vary over time.
7. Unavailability of data necessary to specify the problem.
8. A qualitative description of some of the data.
9. The possibility of unforeseen consequences resulting from the alteration of existing conditions or the imposition of new ones.

By representing the decision problem as analytical model, these difficulties could be overcome by one or several different following strategies:

1. The creation of a single performance (or objective) function.
2. Specification of the problem variables.
3. Determination of the exact bounds on the problem variables (or, more generally, on functions of the problem variables).
4. Determination of the functions; forms and the parameters describing the functional form.
5. Resolution of the stochastic (uncertain) elements by creating a deterministic form or probability assessments.
6. Reconciliation of the dynamic nature of the problem and conversion to a static mode, and revising the model periodically.
7. Solution of the data collection problem.
8. Quantification of the data.
9. Inclusion of all-important elements and unforeseen consequences of changes in the problem variables.

A key to success in modelling is the recognition that the model is an abstraction. Models are not constructed to provide the only answer to a decision problem. Instead, they provide information that is helpful in decision making. A model should not have all the complexities of reality. If it did, it would be extremely difficult to solve and would probably provide the decision-maker with little insight or, indeed, information. Conversely, the model should not be so much of an over simplification that it bears little resemblance to the real world. A good model strikes a balance.

All models including verbal, mental, and mathematical contain independent variables, dependent variables, parameters and constants. In verbal models, these elements are put together in a loose and often intuitive fashion, making understanding apparent and communication easy. As one moves from verbal to mental to mathematical models, the relationships between the variables and the parameters become more specific. The degree of specificity needed determines the type of model that will be used in a specific situation.

There are a variety of model types within the classification of mathematical models. Classification of mathematical models as descriptive or normative, static or dynamic, deterministic or stochastic is not idle taxonomy. Since the decision model must be formulated to provide useful information in such a way that the model can be expeditiously solved, it is important for both decision-makers and model builders to be aware of the existing models and their essential features.

The process of model building is an iterative process. No one, even the most experience model builder, develops a usable model in a single, straightforward development. Instead, there is a process of tentative formulation and validation, followed by reformulation and revalidation until a degree of confidence in the usefulness of the model is developed.

1.3.32 Why Analytical Modelling?

We are attempting to 'model' what the reality is so that we can predict it. The tools of applied OR/MS modelling process help to understand the decision problem at hand, determine logical results of the decision, and choose an optimal course of action. Much of this is done with modelling. A model is a representation of a situation. The change in the environment and variables surrounding the decision problem can be studied to determine the effects that they have on the decision problem. Modelling is a kind of simplification of reality intended to promote under-standing of reality. The information learned from the model can then be applied to the real world decision problem. The tasks of the modeller are:

1. To force the decision maker to make his assumptions explicit.
2. To provide a well-defined statement of the problem. The logical processes utilised in OR/MS modelling process force the manager to clarify and define the problem under consideration.
3. To give you the road map, compass, and guide posts to reach what is the most important objective for your company.
4. To provide a frame of reference for solving the central and related problems. OR/MS modelling process relies upon mathematical models of a problem that can be adapted to future problems similar in nature.
5. To provide answers to ‘What-if' types of questions. In some cases a model is a description of some system intended to predict what happens if certain actions are taken.
6. To enable the interpretation of the results and their implications measured in dollars -- the only language manager can understand.
7. To obtain an objective scientific evaluation that is reproducible by others. Since it is a scientific approach based on facts (not belief or opinion), managers can convince others why they made a particular decision. This is called defensible decision-making. Business people deal with facts.
8. To resolve the conflicts of interest among the components of the organisation. The decision maker might incorporate some other perspectives of the problem such as cultural, political, psychological, etc., into the management scientist's recommendations.
9. To assist the manager (the decision maker or the person who has a problem).
10. To provide guidance to managers in their decision-making. OR/MS modelling process allows the manager to minimise the risk associated with an unknown decision outcome.

Logic is the vehicle (the container) for conveying (delivering) ideas (the word logistic derived from logic with a similar but physical meaning) and solutions to other people. Unfortunately, not many people care to learn logic, because everybody already conceives himself or herself to be proficient enough in the science of reasoning. But I observe that this satisfaction is limited to one's own rationalisation, and does not extend to that of other people. Many people use "For example, ..." to prove something, but, "For example" is not a proof. However, a good "Counterexample" could be both necessary and sufficient for disproving a given statement.

Logic is the hygiene of the thinking in decision making modelling process. As I said already, it is also a strong container in which you put your ideas in order to deliver it to others. Logic by itself is nothing it is an empty container. Both are needed -- good ideas and strong logic to communicate them. Having good ideas without strong logic for communication is like silver in the mine.

1.4 Human behaviour and MS/OR

1.4.1 Human being and wishful views

The management scientist is not the decision maker. The decision maker must incorporate other necessary perspectives including the organisational, environmental, conflicting, historical, political, dynamic, and psychological aspects of the problem into the management scientist's analytical model. There are natural nature and human relations which influence behaviour both decision maker and management scentist

Intuition is a mode of fast thinking: Intuition may not always help you in finding the right answer to an even a simple question. Suppose you are filling two ice cube trays with water, boiling hot in one, cold in the other, and placing both in a freezer. The question is: Which tray turns to ice quicker?" If your answer is "the tray with boiling hot water." You are right. But how come? How could you resolve this apparent isolation of the laws of physics.

1.4.2 One problem can have different solutions

Why do different managers make different decisions for a given problem? Why are we all different? Because we all have different experiences and unique backgrounds. Every experience in life shapes our mind in a unique way. Knowledge is a biological phenomenon. Humans experience the world in their own ways. Through their internal processes, each human engages in a creative relationship with the external world, bringing forth a myriad of different models.

The history of science shows how weak common sense, instinct, and intuition can be taken as guides to our understanding. For example, intuition is a truncated logic and it is never clearly justified on a scientific ground.

Conflict is a part of life. People and businesses suffer when conflict is ignored and not managed properly. Relationships are strained, productivity diminishes, and destruction can be the ultimate result. Many of us are so averse to conflict that we practice appeasement at any price, while others cling to adversarial approaches which can escalate all the costs of settling differences. These behaviours are often the spawning ground for further conflict. They occur because we do not know about and how too effectively use the array of possibilities that exist for successful conflict management.

1.4.3 Humans behaviour towards decision making

Behaviour decision making is to understand how people make decisions and how they can make decision making process more effective and efficient. Such as being conservative, our perpetual. The behaviour science are applicable to decision process form both quantitative and qualitative viewpoints to improve a stronger foundation for making better decisions. The decision-maker's style and characteristics can be classified as: The thinker, the cowboy (snap and uncompromising), Machiavellian (ends justifies the means), the historian (how others did it), the cautious (even nervous), etc.

1.4.4 Decision making versus habits

Decision-making involves reaching a conclusion, which implies deliberation and thought and suggests a conscious act. While a natural reaction or unconscious act would be labeled as habit, reflex act, or impulsive act, or habit which is, unfortunately the centre of gravity when we want to start the decision making process.

Power: It is impossible to understand decision maker's behaviour in organisational situation where conflict exists without considering the role of power. Power has a major impact on information, uncertainty, and resources dependency since there is competition among organisation members for the scarce resources.

1.4.5 Evil and unethical decisions

One must certainly beware of the big difference between unethical and evil decisions. The CEO for an internationally known tire company signs off on the production of tires that he knows are likely to disintegrate under certain conditions. Even with such knowledge; yet he makes it clear that this information is not to be publicised and approves production and sales of the tires. Decide whether such a decision is an evil or unethical one? What about this scenario? An administrator in a fascist country follows the orders of his superior and signed off on the death of thousands of innocent men, women and children; but he never personally killed any of those people himself nor would he. Without integrity, no company can have positive word of mouth.

1.4.6 Resistance to decisions

The most universal difficulty arises from people's fear of planned change. People resist changes, more accurately; they resist being changed by other people. Resistance can take the form of either open hostility or covert sabotage of decision-makers efforts. Even the best designed strategy always fail if those who must carry them out refuse to do so.

Do not take a "model" as the "reality": Models are useful but they all certainly come with their own baggage of simplification, and theorisation of reality, however, the price for not modelling is eternal obfuscation. A model could be as good as "virtual reality", however, it is never the "real reality". Unfortunately, in many cases, modelling becomes an end rather than a means. The modeller spends so much time in creating the model that he/she falls in love with the model: the model becomes the reality. Do not take a "model" as the "reality", Unfortunately, many do.

1.4.7 Effective communications skills

The management scientist must know that his/her success depends on effective communications skills (i.e., making common what is individually experienced). Proper focusing on communicating the results and recommended course of action obtained by the modeller is needed. This helps in achieving a consensus concerning acceptable course of action.

1.4.8 A Guide to carrying out the OR/MS model independent on subjective factors

1. What he thinks the problem is; i.e., what kind of system is involved? What is it doing that is undesirable?
2. Why is it undesirable?
3. What decision(s) would the client like to make?
4. How does the problem hinder the function of the client and his/her system in the company?
5. What would your client like you to do for them?

1. How it works/behaves?
2. If the complaint of behaviour occurs as stated?
3. How the people in the system view the problem?

1. What are the interaction relationships among the components of the system?
2. What criteria do these relationships imply for assessing the performance of your client and his/her system?
3. How might the project affect his/her relationships in the organisation?

1. If you can accept the client's account of the system's behaviour.
2. If you can accept the client's criteria for judging the system's behaviour
3. If you have sufficient understanding of the way the system works to identify and consider the effects of possible changes.
4. What you think your client needs from you.
5. Why you cannot immediately satisfy your client's need.
6. If you have done as much as possible to help the client.

1. Having a high tolerance for ambiguity.
2. Having a well-ordered sense of priorities.
3. Being a good listener.
4. Always building the consensus around a decision.
5. Avoiding stereotypes.
6. Remaining resilient with feedbacks.
7. Being comfortable with both soft and hard input.
8. Being realistic about cost and difficulty.
9. Avoiding a decision minefield.

In recent years, there has been increasing concern over the relevance of many aspects of OR/MS modelling process. The predominant paradigm used is that of science aimed at explanation and prediction. However, all too often, management scientists use methods which are increasingly sophisticated and therefore increasingly difficult for the decision maker to relate the problem he/she is experiencing.

Unfortunately, gaps exist between the theory and the application of modelling for decision-making. This statement is, of course, from the perspective of the modellers who recognise the gap and not from the perspective of decision makers. Not all managers are aware of modelling concepts for decision-making or the practice of modelling for decisions.

The evidence for the existence of this gap is the many papers published on modelling. Very few address actual situations and even fewer present validated solutions to recognised problems.

Reason for the Gaps:

There are a number of factors contributing to the existence and even growth of the gap. These include:

1. The real problems are tough to define and usually difficult to analyze and model.
2. As it is easier to make plans than to carry them out, models that are not to be implemented are not drawn up correctly and not taken seriously from the start.
3. Data are often scattered, incomplete, and lacking in accuracy. Some companies are satisfied with "ballpark" results in order to save on the cost and get the results quicker. The "ballpark" results use less data and more assumptions. This approach takes less time to collect and thus saves money as well.
4. Close collaboration between the modeller and the problem owners is required. Collaboration is occurring infrequently since the organisation does not see a direct and often immediate benefit. The organisation also does not have the confidence in the ability to deliver without causing damage in some form. Case experience is helpful in establishing trust and the willingness to cooperate.
5. There exists a need to influence the culture and attitude toward modelling within the business community and this requires a more capable and better-educated manager. Numerous cases exist where a company spends a large amount of dollars on a marketing promotion and a small amount of dollars in researching its effectiveness.
6. Managers are poorly trained in the concepts and/or the use of analytical models.
7. Modellers must especially address the issues labeled as important by the manager from a cost saving perspective.

1. Ignore the problem and go immediately to the solution since that is where the profit lies.
2. There are no small problems, only small budgets.
3. Names are control variables.
4. Clarity of presentation leads to aptness of critique.
5. Invention of the wheel is always on the direct path of a cost plus contract.
6. Undesirable results stem only from bad analyses.
7. It is better to extend an error than to admit to a mistake.
8. Progress is a function of the assumed reference system.
9. Rigorous solutions to assumed problems are easier to sell than assumed solutions to rigorous problems.
10. In desperation address the problems.