Mathematical Problem

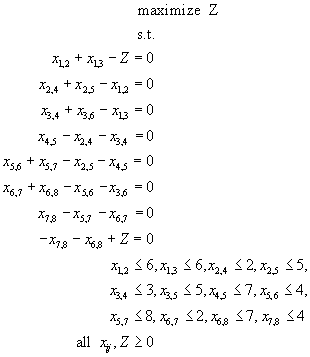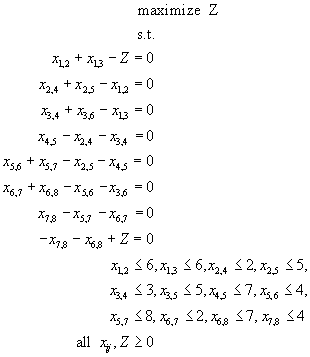
Mathematical Model of the Maximum Flow Problem

The decision variables are defined x_ij, the number of units of flow on arc (i,j). The pipeline capacity limits (problem Aqueduct, Picture 8.3 in level 1) are maximum arc flows, m_ij The model has conservation of flow constraints. For Node 6, the amount of water (in m³) leaving the node is equal to the amount entering the node:

x_6,7 + x_6,8 = x_3,6 + x_5,6

After transposing all variables to the left hand side of the equation, the result is

x_6,7 + x_6,8 - x_3,6 - x_5,6 = 0

The maximum flow problem has no specified net stock position for any node. However, the goal is to maximize the flow from Node 1 to Node 8. Let the net stock position at Node 1 be +Z, and let the net stock position at Node 8 be -Z. The amount Z is a decision variable, and you define it as the maximum flow amount. In the maximum flow problem, the decision variables are Z and the flows for each arc.

The constraint for Node 1 is

x_1,2 + x_1,3 = Z

After transposing a decision variable Z to the left hand side of the equation, the result is

x_1,2 + x_1,3 – Z = 0

The entire linear programming model is