The cost per unit shipped from Node i to Node j is c_ij, and the maximum capacity from Node i to Node j is m_ij Think of a network problem as the reallocation of units among the cities by shipping quantities over the roads. The decision variable for Arc (i, j) is represented as x_ij, the number of units shipped from Node i to
Node j. Each node has a net stock position showing the excess or shortage of product at that node.
 
 

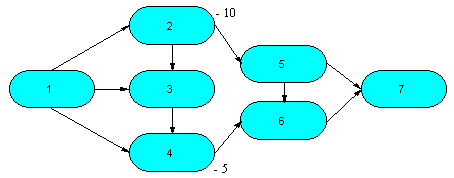
For the following picture, Node 2 has a net stock position of - 10, which we write at the node. You need to ship 10 units to Node 2 to satisfy the requirement at that city. There is a conservation of flow constraint for each node. That is, the total amount remaining at a node plus the amount shipped out of it equals the amount initially at the node plus the amount shipped into it. Because the net stock position of Node 2 is - 10, you need to leave 10 units there by reallocating units from nodes that have an excess.
 
 

As an example, let's write the conservation of flow constraint for Node 2. Node 2 is connected to Node 1 by an incoming arc and to Nodes 3 and 5 by outgoing arcs. If there are no units initially at Node 2 but we desire to drop off 10 units, the conservation of flow constraint is

The constraint says that the total of the outgoing material plus the 100 units that must be dropped off has to equal the total of the incoming material. When written in the standard form, the constraint is

The arc capacity constraints are

Sometimes, an arc has a minimum amount that is greater than 0. For example, you might make a policy decision to ship at least some minimal amount between two cities to maintain good relations with a transportation service. Or you might have a contract specifying a minimum shipment. If the minimum is greater than 0, let n_ij represent it for Variable x_ij . The minimum constraint is

Let's relate the above terminology to the real situation of grain and cereal products. The nodes are farms, distribution centers, mills, and bakeries. The arcs are transportation links connecting the nodes. Some of the nodes are connected by boats, some by trains, and some by trucks. The arcs have costs for shipping products. The boats, trains, and trucks have capacity limits. Gathered grain is reallocated from farms to distribution centers that serve mills. The net stock position is negative at distribution centers that require grain. The net stock position is positive at farms that have excess product (grain) available. This network model maximizes the profit for grain distributing and processing. Profit maximization is the objective because the model is also used for pricing decisions. The total revenue is not fixed and a price change affects the demand for the agricultural products.