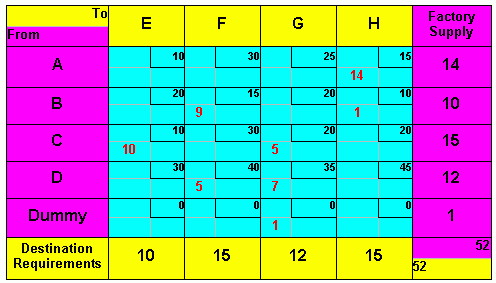
Closed path "a"
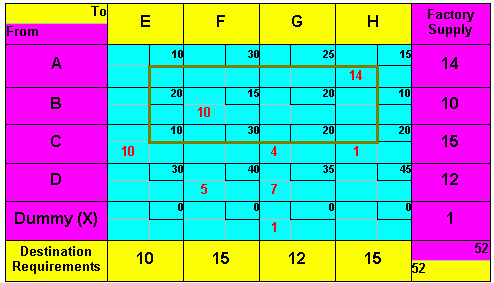
Closed path "b"
Step 1: Pick any empty cell and identify the closed path leading to that cell. A closed path consists of horizontal and vertical lines leading from an empty cell back to itself (If assignments have been made correctly, the matrix has only one closed path for each empty cell.) In the closed path there can only be one empty cell that we are examining. The 90-degree turns must therefore occur at those places that meet this requirement. Two closed paths are identified. Closed path a is required to evaluate empty cell A-E; closed path b is required to evaluate empty cell A-F.


Step 2: Move one unit into the empty cell from a filled cell at a corner of the closed path and modify the remaining filled cells at the other comers of the closed path to reflect this move. (More than one unit could be used to test the desirability of a shift. However, since the problem is linear, if it is desirable to shift one unit, it is desirable to shift more than one, and vice versa.) Modifying entails adding to and subtracting from filled cells in such a way that supply and demand constraints are not violated. This requires that one unit always be subtracted in a given row or column for each unit added to that row or column. Thus, the following additions and subtractions would be required :
For the path a:
For cell A-E, the pluses and minuses are
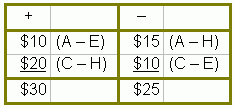
For cell A-H, the pluses and minuses are

Thus in both cases it is apparent that no move into
either empty cell should be made.
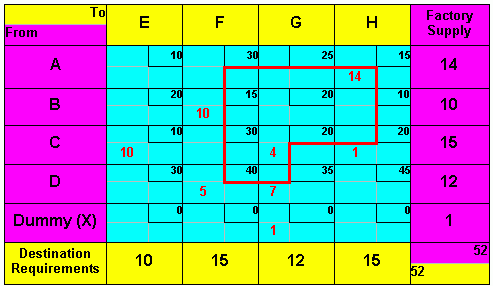
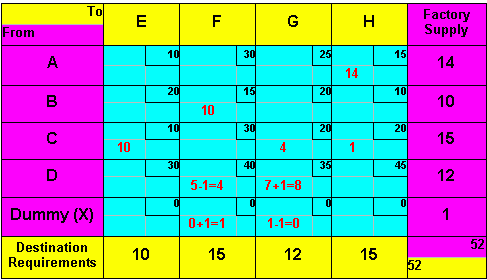
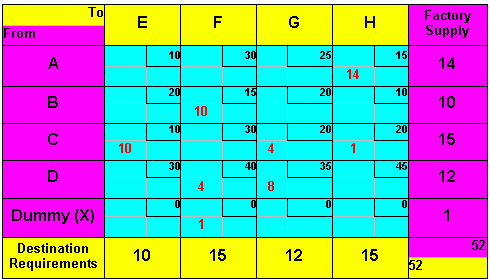
Step 4: Repeat Steps 1 through 3 until all empty cells have been evaluated. To illustrate the mechanics of carrying out a move, consider cell X-F and the closed path leading to it, which is a short one: X-G, D-G, and D-F. The pluses and minuses are
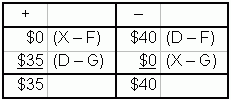
Since there is a savings of $5 per unit from shipping
via X-F, as many units as possible should be moved into this cell. In this
case, however, the maximum amount that can be shifted is one unit—because
the
maximum amount added to any cell may not exceed the quantity found in the
lowest-amount cell from which a subtraction is to be made. To do otherwise
would violate the supply and demand constraints of the problem. Here
we see that the limiting cell is X-G since it contains only one unit.
The pluses and minuses are
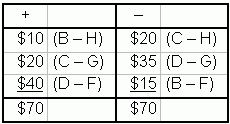
Since there is a savings of $0 (70 - 70) per unit
from shipping via B-H, we obtain a different – "alternate
optimal solution" with the same transportation cost (next
table).