The Exponential Distribution

In connection with the Poisson process, we have discussed the Poisson probability distribution, which gives the probability of the number of occurrences of an event, given an intensity  and a certain time period t. For the same Poisson process, we could ask about the waiting time between successive events (that is, the interarrival time). In other words, what is the probability distribution of time, t, between events? This probability distribution is called the exponential distribution (see Figure).
 


Exponential Probability Density Function



The exponential probability density function is:

 
The mean of the exponential distribution is
E(t) =  ,
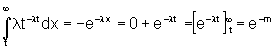and the variance is D(t) = . The right hand tail of the exponential distribution is

,

where m = t.

The probability that the time between events (arrivals) is greater than t is e-m. Note that this is also the value of a Poisson mass function for zero occurrences (arrivals) in a time period t.

The Poisson distribution for arrivals per unit of time and the exponential distribution for interarrival times provide two alternative ways of describing the same thing. We can say that the number of arrivals per unit is Poisson with mean rate  = 5 per hour, for example; alternatively, we can say that the interarrival times are exponentially distributed with mean interarrival time µ = (1/) = 1/5 hour; each statement implies the other.