
Obr√°zek 1.1 ‚ÄĚProces rozhodov√°n√≠‚ÄĚ
Uńćebn√≠ c√≠le
Po prostudov√°n√≠ t√©to kapitoly byste mńõli b√Ĺt schopni:
Definice Management Science uv√°d√≠, Ňĺe jde o aplikaci vńõdeck√Ĺch metod, technik a prostŇôedkŇĮ pŇôi Ňô√≠zen√≠ operac√≠ v syst√©mu s c√≠lem zajistit optim√°ln√≠ ŇôeŇ°en√≠ probl√©mu v syst√©mu. Management Science zahrnuje dalŇ°√≠ vńõdeck√© discipl√≠ny, kter√© maj√≠ spoleńćn√Ĺ c√≠l: aplikaci vńõdeck√Ĺch metod pŇôi anal√Ĺze a ŇôeŇ°en√≠ manaŇĺersk√Ĺch rozhodovac√≠ch probl√©mŇĮ. V t√©to kapitole se soustŇôed√≠me na tyto discipl√≠ny:
1.1. Management Science
1.1.1. Úvodní poznámky
1. V n√°zvu Management Science jsou obsaŇĺena dvńõ slova: management a science (vńõda). N√°zev pŇôedmńõtu tedy napov√≠d√°, Ňĺe se jedn√° o disciplinu, kter√° vyuŇĺ√≠v√° vńõdeck√© pŇô√≠stupy pŇôi ŇôeŇ°en√≠ probl√©mŇĮ Ňô√≠zen√≠.
2. Pod pojmem management budeme d√°le rozumńõt proces, kter√Ĺm se dosahuje splnńõn√≠ urńćit√Ĺch c√≠lŇĮ pomoc√≠ vyuŇĺ√≠v√°n√≠ zdrojŇĮ - lid√≠, penńõz, energie, materi√°lŇĮ, prostoru a ńćasu. Zdroje pŇôedstavuj√≠ vstupy tohoto procesu a dosaŇĺen√≠ c√≠lŇĮ jeho v√Ĺstupy.
3. StupeŇą √ļspńõŇ°nosti manaŇĺersk√© pr√°ce lze mńõŇôit velikost√≠ pomńõru mezi vstupy a v√Ĺstupy. Tento pomńõr je m√≠rou produktivity ńćinnosti organizace. Produktivita je povaŇĺov√°na za jeden z nejdŇĮleŇĺitńõjŇ°√≠ch ukazatelŇĮ fungov√°n√≠ organizace. Produktivita vŇ°ech organizac√≠ a jednotlivcŇĮ v dan√©m st√°tńõ pŇôedstavuj√≠ ve sv√©m souńćtu celkovou Ňĺivotn√≠ √ļroveŇą (well-being) obyvatelstva.
4. Produktivita organizace, tj. √ļspńõŇ°nost managementu, z√°vis√≠ na realizaci manaŇĺersk√Ĺch funkc√≠: pl√°nov√°n√≠, organizaci, veden√≠ a Ňô√≠zen√≠. ManaŇĺersk√© funkce pŇôedstavuj√≠ v organizaci permanentn√≠, kontinu√°ln√≠ proces, kter√Ĺ je charakterizov√°n permanentn√≠m a kontinu√°ln√≠m rozhodov√°n√≠m. V tomto smyslu mŇĮŇĺeme management organizace povaŇĺovat za ekvivalentn√≠ rozhodov√°n√≠.
5. Z historick√©ho hlediska byl management - rozhodov√°n√≠ povaŇĺov√°n za umńõn√≠, manaŇĺer z√≠sk√°val svoje schopnosti spr√°vnńõ rozhodovat dlouhodobou prax√≠, zkuŇ°enost√≠, talentem. Z toho dŇĮvodu byly v managementu vypracov√°ny rŇĮzn√© styly Ňô√≠zen√≠ pro rŇĮzn√© typy organizac√≠. Tyto styly jsou ńćasto zaloŇĺeny na tvoŇôivosti, osobnosti, intuici, zkuŇ°enosti. ProstŇôed√≠, v nńõmŇĺ management pŇĮsob√≠, se v posledn√≠ch l√©tech radik√°lnńõ mńõn√≠. Organizace se zvńõtŇ°uj√≠, roste konkurence, vnitŇôn√≠ vztahy v organizaci i jej√≠ okol√≠ obsahuj√≠ prvky nejistoty. Management - dŇô√≠ve povaŇĺovan√Ĺ za umńõn√≠ a vyuŇĺ√≠vaj√≠c√≠ zkuŇ°enost - se v√≠ce soustŇôeńŹuje na systematick√Ĺ a analytick√Ĺ pŇô√≠stup k rozhodov√°n√≠. V tabulce 1.1 jsou uvedeny z√°kladn√≠ faktory, kter√© pŇĮsob√≠ na organizaci a vynucuj√≠ si zmńõny tradińćn√≠ho pŇô√≠stupu k rozhodov√°n√≠.
Z tabulky 1.1 je zŇôejm√©, Ňĺe rozhodov√°n√≠ je v
souńćasnosti mnohem komplikovanńõjŇ°√≠ a sloŇĺitńõjŇ°√≠ proces, neŇĺ tomu
bylo dŇô√≠ve:
|
|
|
|
|
Informańćn√≠ syst√©my V√Ĺpońćetn√≠ technika |
|
|
|
Organizańćn√≠ struktury Konkurenńćn√≠ prostŇôed√≠ |
|
|
|
PoŇĺadavky spotŇôebitelŇĮ St√°tn√≠ intervence |
|
|
Tabulka 1.1 ‚ÄĚFaktory, ovlivŇąuj√≠c√≠ rozhodov√°n√≠
manaŇĺera‚ÄĚ
(Turban E., Meredith
R.J.: Fundamentals of Management Science)
a) Pońćet alternativ moŇĺn√Ĺch ŇôeŇ°en√≠, kter√© nab√≠zej√≠ rozv√≠jej√≠c√≠ se informańćn√≠ syst√©my, je zpravidla znańćn√Ĺ a jejich v√Ĺbńõr jiŇĺ nelze prov√°dńõt intuitivnńõ - je tŇôeba pouŇĺ√≠t exaktn√≠ metody v√Ĺbńõru, ovńõŇôit riziko rozhodnut√≠, organizovat implementaci alternativy ŇôeŇ°en√≠ ve velmi sloŇĺit√Ĺch podm√≠nk√°ch trhu.
b) V√Ĺbńõr alternativy ŇôeŇ°en√≠ je zpravidla podŇô√≠zen v√≠ce rŇĮzn√Ĺm kriteri√≠m, kter√© kromńõ zisku organizace rovnńõŇĺ zohledŇąuj√≠ soci√°ln√≠, tradińćn√≠, kulturn√≠ a politick√© aspekty.
c) Rozhodov√°n√≠ prob√≠h√° za nejistoty. ManaŇĺer nem√° k disposici vŇ°echny potŇôebn√© informace o souńćasn√©m a zejm√©na o budouc√≠m chov√°n√≠ sv√©ho okol√≠.
d) Cena, kterou organizace zaplat√≠ za nespr√°vn√© rozhodnut√≠ sv√©ho managementu, je znańćnńõ vysok√° v dŇĮsledku mnohostrann√©ho propojen√≠ organizace se sv√Ĺm okol√≠m, neboŇ• chybn√© rozhodnut√≠ v jedn√© organizaci m√° za n√°sledek Ňôetńõzen√≠ dalŇ°√≠ch chyb v dalŇ°√≠ch navz√°jem propojen√Ĺch organizac√≠ch.
6. Exaktn√≠ metody a pŇô√≠stupy, kter√© vyuŇĺ√≠v√° soudob√Ĺ management pro podporu rozhodov√°n√≠, jsou soustŇôedńõny ve vńõdn√≠ disciplinńõ, kter√° se naz√Ĺv√° Management Science.
Existuje nńõkolik definic Management Science. Uvedeme dvńõ klasick√© definice:
1.1.2. Definice
a) Churchman, Ackoff, Arnoff: ‚ÄúManagement Science/Operation Research je aplikace vńõdeck√Ĺch metod, technik a prostŇôedkŇĮ (tools) pŇôi Ňô√≠zen√≠ operac√≠ v syst√©mu s c√≠lem optim√°ln√≠ho ŇôeŇ°en√≠ probl√©mŇĮ v syst√©mu‚ÄĚ.
b) The Commitee on Operation Research of the National Research Council in Great Britain: ‚ÄúAplikace vńõdeck√Ĺch metod pŇôi anal√Ĺze operac√≠ (to the study of operations) ve velk√Ĺch, komplexn√≠ch organizac√≠ch a instituc√≠ch‚ÄĚ.
1.1.3. Pozn√°mky k definici
1. V dalŇ°√≠m textu budeme pod n√°zvem Management Science rozumńõt aplikaci vńõdeck√Ĺch metod pŇôi anal√Ĺze a ŇôeŇ°en√≠ manaŇĺersk√Ĺch rozhodovac√≠ch probl√©mŇĮ.
2. V souńćasn√© dobńõ existuje v√≠ce rŇĮzn√Ĺch n√°zvŇĮ pro Management Science, kter√© s mal√Ĺmi v√Ĺjimkami pŇôedstavuj√≠ stejnou vńõdn√≠ discipl√≠nu. Je to proto, Ňĺe se jedn√° o velmi mladou vńõdu a nedoŇ°lo dosud ke konsensu, do jak√© oblasti vlastnńõ patŇô√≠. V podstatńõ ekvivalentn√≠ n√°zvy pro Management Science jsou:
Operańćn√≠ v√Ĺzkum (Operations Research - OR). N√°zev se zpravidla uŇĺ√≠v√°, m√°me-li na mysli rozvoj matematick√Ĺch z√°kladŇĮ Management Science, zat√≠mco Management Science se soustŇôeńŹuje v√≠ce na metodologie a aplikace.
Operańćn√≠ anal√Ĺza (Operation Analysis).
Kvantitaivn√≠ anal√Ĺza, Kvantitativn√≠ metody (Quantitative Analysis/Methods). N√°zev se pouŇĺ√≠v√° ńćasto v oblasti marketingu a financ√≠.
Syst√©mov√° anal√Ĺza (System Analysis).
Operańćn√≠ management (Operations Management). Od r. 1980 se rozv√≠j√≠ v oblasti marketingu s dŇĮrazem na optim√°ln√≠ Ňô√≠zen√≠ vŇ°ech operac√≠ od zańć√°tku v√Ĺrobn√≠ho procesu aŇĺ ke spotŇôebiteli s c√≠lem zajistit maxim√°ln√≠ kvalitu koneńćn√©ho produktu a maxim√°ln√≠ spokojenost spotŇôebitele. DŇĮraz na spokojenost spotŇôebitele a √ļcta k nńõmu je pro metodologie Operańćn√≠ho managementu typick√°!
3. N√°zev Management Science v ńćesk√©m pŇôekladu jako "ManaŇĺersk√° vńõda" nevystihuje dobŇôe roli, kterou tato disciplina v managementu m√° - podporovat procesy rozhodov√°n√≠. Z toho dŇĮvodu je vhodn√© uŇĺ√≠vat pŇĮvodn√≠ nepŇôeloŇĺen√Ĺ n√°zev. V dalŇ°√≠m textu budeme uŇĺ√≠vat zkratky Management Science - MS.
1.1.4. Základní charakteristiky MS
1) Podpora rozhodování (v managemenmtu, marketingu,
ekonomice aj.).
2) VyuŇĺ√≠v√°n√≠ vńõdeck√Ĺch postupŇĮ.
3) Syst√©mov√Ĺ pŇô√≠stup k ŇôeŇ°en√≠ probl√©mŇĮ.
4) T√Ĺmov√° spolupr√°ce (Interdisciplin√°rn√≠ a
transdisciplinární spolupráce).
5) PouŇĺ√≠v√°n√≠ matematick√Ĺch modelŇĮ.
6) VyuŇĺ√≠v√°n√≠ Informatiky a V√Ĺpońćetn√≠ techniky.
1.1.5. Poznámky k základním charakteristikám MS
1. Syst√©mov√Ĺ pŇô√≠stup. ŇėeŇ°en√≠
probl√©mu lze charakterizovat jako komplexn√≠ celostn√≠ pŇô√≠stup. ZdŇĮrazŇąuje
se komplexn√≠ ch√°p√°n√≠ jevŇĮ a procesŇĮ ve vŇ°ech jejich podstatn√Ĺch
vnitŇôn√≠ch i vnńõjŇ°√≠ch souvislostech. Je to uspoŇô√°dan√Ĺ princip myŇ°len√≠
ńći jedn√°n√≠, kter√Ĺ m√° pevn√Ĺ myŇ°lenkov√Ĺ Ňô√°d. Oproti nńõmu lze nesyst√©mov√Ĺ
pŇô√≠stup charakterizovat jako Ňĺiveln√Ĺ, kdy myŇ°lenkov√Ĺ postup je voln√Ĺ,
myŇ°lenkov√Ĺ proces je subjektivn√≠ a individu√°lnńõ utv√°Ňôen√Ĺ. Syst√©mov√Ĺ
pŇô√≠stup mŇĮŇĺe zv√ĹŇ°it efektivnost syst√©mu aŇĺ o 40%, zat√≠mco klasick√©
pŇô√≠stupy jen o 10-15%.
2. T√Ĺmov√° pr√°ce. Vych√°z√≠ ze z√°sady,
Ňĺe Ňĺ√°dn√Ĺ jednotliv√Ĺ pracovn√≠k nemŇĮŇĺe obs√°hnout vŇ°echny vńõdecky
pouŇĺiteln√© poznatky, ale skupina je toho schopn√°. Tento pŇô√≠stup odpov√≠d√°
pŇô√≠slov√≠: ‚Äúv√≠ce hlav - v√≠ce rozumu‚ÄĚ. T√Ĺmy MS jsou sloŇĺeny ze
specialistŇĮ rŇĮzn√©ho odborn√©ho zamńõŇôen√≠. JestliŇĺe ńćlenov√© kolektivu
poch√°zej√≠ z rŇĮzn√Ĺch oborŇĮ, lze t√≠m zn√°sobit pońćet moŇĺn√Ĺch metod
pŇô√≠stupu k ŇôeŇ°en√≠. Zapojen√≠m specialistŇĮ rŇĮzn√©ho zamńõŇôen√≠ do
ŇôeŇ°en√≠ probl√©mu se t√©Ňĺ dosahuje komplexnńõjŇ°√≠ho pohledu na probl√©m.
(Consolidated wisdom - spojen√© vńõdńõn√≠).
3. PouŇĺit√≠ modelov√© a v√Ĺpońćetn√≠ techniky.
Jde o studium sloŇĺit√Ĺch jevŇĮ re√°ln√©ho svńõta na zjednoduŇ°en√Ĺch a
√ļńćelovńõ konstruovan√Ĺch modelech. Model m√° objasnit situaci, nejen
ji pouze popsat. Matematick√© modely vyuŇĺ√≠van√© v OA maj√≠
nejrŇĮznńõjŇ°√≠ tvar, ale jejich podstata je stejn√°. V koneńćn√© √ļpravńõ
model pŇôedstavuje matematick√© sch√©ma (napŇô. soustavu line√°rn√≠ch rovnic),
kter√© popisuje dan√Ĺ syst√©m. V√Ĺpońćty modelŇĮ je nutno realizovat pomoc√≠
v√Ĺpońćetn√≠ techniky. V souńćasn√© dobńõ je k dispozici dostateńćn√Ĺ hardware
i software.
4. PouŇĺit√≠ rŇĮzn√Ĺch metod a algoritmŇĮ.
PŇôi ŇôeŇ°en√≠ konkr√©tn√≠ch probl√©mŇĮ vyuŇĺ√≠v√° MS kombinaci rŇĮzn√Ĺch
metod a technik. Pro nńõkter√© typick√© ńćasto se opakuj√≠c√≠ probl√©my
byla vypracov√°na Ňôada speci√°ln√≠ch metod. Naz√Ĺv√°me je metodami Management
Science, resp. Ekonomicko matematick√Ĺmi metodami (EMM). Metody jsou upraveny
do standardn√≠ch algoritmŇĮ.
1.1.6 Historick√° pozn√°mka
JiŇĺ ve 20. letech tohoto stolet√≠ bylo zŇôejm√©, Ňĺe se metody a techniky Ňô√≠zen√≠ opoŇĺńŹuj√≠ ve sv√©m v√Ĺvoji za rozvojem v√Ĺrobn√≠ techniky. Ke spojen√≠ vńõdy s prax√≠ na √ļseku Ňô√≠zen√≠ doŇ°lo v prŇĮbńõhu 2. svńõtov√© v√°lky, kdy velitel√© vojensk√Ĺch jednotek byli jmenov√°ni do funkc√≠ ŇôeditelŇĮ prŇĮmyslov√Ĺch podnikŇĮ. V arm√°dńõ se rozvinula rozs√°hl√° dńõlba pr√°ce, nastoupila tńõsn√° kooperace rŇĮzn√Ĺch druhŇĮ zbran√≠ atd. Bylo tŇôeba zcela nov√©ho pŇô√≠stupu k organizaci, pl√°nov√°n√≠ a Ňô√≠zen√≠ ńćinnost√≠ sloŇĺit√©ho syst√©mu arm√°dy.
V roce 1938 byly zah√°jeny prvn√≠ v√Ĺzkumn√© pr√°ce ve Velk√© Brit√°nii, kter√© mńõly charakter operańćn√≠ho v√Ĺzkumu. Zkoumal se zde zpŇĮsob spr√°vn√©ho syst√©mu nasazen√≠ radarŇĮ v protileteck√© obranńõ. V roce 1939 pak byla v r√°mci RAF (Kr√°lovsk√©ho letectva) vytvoŇôena prvn√≠ skupina operańćn√≠ho v√Ĺzkumu. Postupnńõ zańćaly vznikat dalŇ°√≠ obdobn√© skupiny u ostatn√≠ch zbran√≠. Kromńõ ryze vojensk√Ĺch probl√©mŇĮ ŇôeŇ°ily skupiny i celou Ňôadu ot√°zek organizańćn√≠ch a ekonomick√Ĺch (napŇô. dopravn√≠ probl√©m, z√°sobovac√≠, ot√°zky √ļdrŇĺby a obnovy techniky atd.).
Po ukonńćen√≠ v√°lky zańćaly metody operańćn√≠ho v√Ĺzkumu pronikat i do civiln√≠ho prŇĮmyslu. Po roce 1950, kdy se rozŇ°√≠Ňôilo pouŇĺ√≠v√°n√≠ pońć√≠tańćŇĮ, se v z√°padn√≠ch st√°tech zańćalo velmi intenzivnńõ rozv√≠jet uplatŇąov√°n√≠ operańćn√≠ anal√Ĺzy. U n√°s se prvn√≠ pr√°ce na √ļseku operańćn√≠ anal√Ĺzy objevuj√≠ po roce 1955 a kolem roku 1960 zańćaly vznikat prvn√≠ skupiny operańćn√≠ anal√Ĺzy. Od r. 1970 se pro aplikace metod operańćn√≠ho v√Ĺzkumu zańćal pouŇĺ√≠vat term√≠n Mnagement science, pro rozvoj teorie a metodologie term√≠n Operańćn√≠ v√Ĺzkum.
V ńĆech√°ch byly metody MS rozv√≠jeny na vysok√Ĺch Ň°kol√°ch a ńĆSAV. Mezi propag√°tory a prŇĮkopn√≠ky patŇôili zejm√©na Prof. Habr, Prof. Kadlec, Prof. NoŇĺińćka. D√≠ky sv√© matematick√© podstatńõ a v pońć√°teńćn√≠ch f√°z√≠ch rozvoje i dŇĮrazu na matematickou teorii algoritmŇĮ metody se mohly rozv√≠jet i bńõhem totalitn√≠ho politick√©ho reŇĺimu. Nńõkter√© v√Ĺsledky ńćesk√© Ň°koly OR/MS jsou dnes ve svńõtńõ vŇ°eobecnńõ uzn√°v√°ny.
1.2. ManaŇĺersk√© rozhodov√°n√≠
1.2.1. Úvodní poznámka
Teorie rozhodov√°n√≠ (Decision Theory) je vńõdn√≠ discipl√≠na, tvoŇô√≠c√≠ soubor poznatkŇĮ a metod, kter√© mohou usnadnit optim√°ln√≠ rozhodnut√≠. V t√©to souvislosti je tŇôeba upozornit na Ň°irŇ°√≠ v√Ĺznam term√≠nu optim√°ln√≠, kter√Ĺ nńõkteŇô√≠ autoŇôi ch√°pou jako rozhodnut√≠ oproŇ°tńõn√© od chyb nebo prostńõ jako ‚Äúdobr√©‚ÄĚ rozhodnut√≠ podle subjektivn√≠ pŇôedstavy.
Podstatnou ńć√°st teorie optim√°ln√≠ho rozhodov√°n√≠ tvoŇô√≠ vyuŇĺ√≠v√°n√≠ kvantitativn√≠ch metod a modelŇĮ Management Science a Syst√©mov√© anal√Ĺzy. Jde o analytick√© n√°stroje, kter√© poskytuj√≠ integruj√≠c√≠ pŇô√≠stup k rozhodov√°n√≠.
Rozvoj teorie rozhodov√°n√≠ nastal v pades√°t√Ĺch letech, kdy zańćaly vznikat sloŇĺit√© matematick√© a statistick√© n√°stroje a kdy doŇ°lo t√©Ňĺ k oŇĺiven√≠ z√°jmu o soci√°ln√≠ vńõdy.
1.2.2 Podstata rozhodovacího procesu
Rozhodov√°n√≠ pŇôedstavuje dynamick√Ĺ vńõdom√Ĺ proces v√Ĺbńõru jedn√© z moŇĺn√Ĺch alternativ, kterou lze dos√°hnout poŇĺadovan√©ho c√≠le. Rozhodovac√≠ proces je ńćinnost Ňô√≠d√≠c√≠ch pracovn√≠kŇĮ, pŇôi n√≠Ňĺ usiluj√≠ doj√≠t k z√°vńõrŇĮm a rozhodnut√≠m.
Rozhodov√°n√≠ je vyvrcholen√≠m duŇ°evn√≠ch pochodŇĮ, kter√© vedou k z√°vńõru nebo rozhodnut√≠. √öspńõch Ňô√≠d√≠c√≠ch pracovn√≠kŇĮ pŇôi rozhodov√°n√≠ z√°vis√≠ v podstatńõ na schopnosti vykon√°vat dvńõ funkce: analyzovat probl√©m a uńćinit rozhodnut√≠. Informace jsou pŇôi tom surovinou, kter√° se mus√≠ vńõdomńõ a systematicky zpracovat.
KaŇĺd√Ĺ manaŇĺersk√Ĺ rozhodovac√≠ probl√©m vyŇĺaduje, aby byl zkoum√°n z hlediska kvantitativn√≠ho a kvalitativn√≠ho, jak je schematicky zobrazeno na obr√°zku 1.1.

Obr√°zek 1.1 ‚ÄĚProces rozhodov√°n√≠‚ÄĚ
PŇôi kvantitativn√≠ anal√Ĺze se vyuŇĺ√≠vaj√≠ exaktn√≠ matematick√© metody, pŇôi kvalitativn√≠ anal√Ĺze se vyuŇĺ√≠vaj√≠ neformalizovan√© metody, pŇôi nichŇĺ se vyuŇĺ√≠vaj√≠ heuristick√© postupy, panelov√© diskuse, skupiny expertŇĮ apod. PotŇôebn√© informace mus√≠ b√Ĺt shromaŇĺńŹov√°ny souńćasnńõ a posuzov√°ny z hlediska dan√©ho probl√©mu. C√≠lem je pŇôijmout rozhodnut√≠ na z√°kladńõ tńõchto informańćn√≠ch zdrojŇĮ.
1.2.3. Teorie rozhodování
Procesy rozhodov√°n√≠ zkoum√° vńõdn√≠ disciplina Teorie rozhodov√°n√≠ (Decision Theory), jej√≠mŇĺ zakladatelem je H. Simon. Teorie rozhodov√°n√≠ se rozv√≠j√≠ od r. 1960 v r√°mci psychologick√Ĺch vńõd s pŇô√≠m√Ĺmi aplikacemi v ekonomii, managementu, marketingu a financ√≠ch a v soci√°ln√≠ch a politick√Ĺch vńõd√°ch. Pro ŇôeŇ°en√≠ praktick√Ĺch probl√©mŇĮ je vhodn√© ztotoŇĺnit pojem rozhodov√°n√≠ s pojmem ŇôeŇ°en√≠ probl√©mu.
Simon, H.A.: The New Science of Management Decision. Harper and Brothers, New York, 1960.
1.2.4. Klasifikace rozhodovacích situací
Podle Simona lze vŇ°echny rozhodovac√≠ procesy klasifikovat
podle kvality informace, jeŇĺ je pŇôi rozhodov√°n√≠ k disposici do tŇô√≠
kategorií na rozhodovací procesy
a) dobŇôe strukturovan√©,
b) nestrukturované,
c) semistrukturované.
a) DobŇôe strukturovan√© rozhodov√°n√≠, dobŇôe strukturovan√Ĺ probl√©m (well structured, well programmed decision making)pŇôedstavuje rozhodovac√≠ situaci, kdy je k disposici vŇ°echna potŇôebn√° informace, jsou zn√°my postupy, metody a algoritmy ŇôeŇ°en√≠, jsou zn√°ma ŇôeŇ°en√≠ analogick√Ĺch situac√≠. Jedn√° se o oblast rutinn√≠ho, standardn√≠ho rozhodov√°n√≠, intuitivn√≠ rozhodov√°n√≠ zde nem√° smysl.
b) Nestrukturovan√© rozhodov√°n√≠, nestrukturovan√Ĺ probl√©m (unstructured, decision making) pŇôedstavuje situaci, kdy je k disposici informace ne√ļpln√° a nespolehliv√°. Probl√©m je formulov√°n v√°gnńõ, mlhavńõ (fuzzy problem). Nejsou zn√°my analogick√© postupy, nelze aplikovat ovńõŇôen√© a provńõŇôen√© metody ŇôeŇ°en√≠. Intuitivn√≠ rozhodov√°n√≠ pŇôevaŇĺuje.
c) Semistrukturovan√© rozhodov√°n√≠, semistrukturovan√Ĺ probl√©m (semi/ill-structured, decision making) pŇôedstavuje Ň°irok√© spektrum situac√≠ mezi dobŇôe strukturovan√Ĺm a nestrukturovan√Ĺm rozhodov√°n√≠m.
1.2.5 PŇô√≠klad
Jako pŇô√≠klad dobŇôe strukturovan√Ĺch rozhodovac√≠ch probl√©mŇĮ lze uv√©st rozhodov√°n√≠ o v√Ĺrobn√≠ struktuŇôe podniku, o vyt√≠Ňĺen√≠ v√Ĺrobn√≠ linky, stanoven√≠ velikosti objedn√°vky materi√°lu aj.
PŇô√≠kladem nestrukturovan√Ĺch rozhodovac√≠ch probl√©mŇĮ jsou probl√©my ŇôeŇ°en√© na vyŇ°Ň°√≠ch √ļrovn√≠ch Ňô√≠zen√≠, jako je napŇô√≠klad rozhodov√°n√≠ o vytvoŇôen√≠ spoleńćn√©ho podniku, rozhodov√°n√≠ o organizańćn√≠ struktuŇôe, o technologick√Ĺch inovac√≠ch aj. V t√©to skupinńõ probl√©mŇĮ nńõkter√© faktory ovlivŇąuj√≠c√≠ ŇôeŇ°en√≠ nejsou pŇôesnńõ zn√°my, existuje vńõtŇ°√≠ pońćet krit√©ri√≠ pro hodnocen√≠ variant a n√°hodnost zmńõn.
1.2.6. F√°ze
rozhodovacího procesu
Rozhodov√°n√≠ (ŇôeŇ°en√≠ probl√©mu) prob√≠h√° v
ńćase. Simon rozliŇ°uje v prŇĮbńõhu rozhodov√°n√≠ tŇôi f√°ze rozhodovac√≠ho
procesu:
a) Identifikace probl√©mu (Intelligence). Dokonal√© vymezen√≠ probl√©mu. Exaktn√≠ formulace c√≠lŇĮ, anal√Ĺza omezuj√≠c√≠ch a podpŇĮrn√Ĺch prostŇôedkŇĮ. Anal√Ĺza vlastn√≠ organizace a bl√≠zk√©ho i vzd√°lenńõjŇ°√≠ho okol√≠ z hlediska uvaŇĺovan√Ĺch z√°mńõrŇĮ.
b) Anal√Ĺza a ŇôeŇ°en√≠ probl√©mu (Design). Anal√Ĺza identifikovan√©ho probl√©mu, tvorba rŇĮzn√Ĺch alternativ ŇôeŇ°en√≠.
c) V√Ĺbńõr ŇôeŇ°en√≠ (Choice). V√Ĺbńõr nejvhodnńõjŇ°√≠ho ŇôeŇ°en√≠ pro dan√Ĺ probl√©m a organizaci v dan√©m ńćase.
PŇôi kvalitn√≠m rozhodov√°n√≠ je nutno
respektovat vŇ°echny tŇôi f√°ze rozhodovac√≠ho procesu a vńõnovat jim stejnou
pozornost:
a) ŇėeŇ°itel nem√° dostatek informac√≠, a proto je k dispozici mal√Ĺ pońćet variant ŇôeŇ°en√≠ a varianty jsou npŇôenosn√©.
b) ŇėeŇ°itel poŇĺaduje vńõtŇ°√≠ mnoŇĺstv√≠ informac√≠, neŇĺ je nezbytnńõ nutn√© pro nalezen√≠ vŇ°ech pŇôijateln√Ĺch dobr√Ĺch variant ŇôeŇ°en√≠, a t√≠m se ŇôeŇ°en√≠ prodraŇĺuje a prodluŇĺuje.
c) ŇėeŇ°itel pouŇĺ√≠v√° nevhodn√© metody, snaŇĺ√≠
se vtńõsnat probl√©m do zn√°m√©ho algoritmu, t√≠m probl√©m zjednoduŇ°uje
a pŇôedkl√°d√° ve f√°zi v√Ĺbńõru varianty ŇôeŇ°en√≠ jin√©ho probl√©mu.
V teorii rozhodov√°n√≠ se popisuje tzv. ‚ÄúParadigma omezen√© racionality‚ÄĚ (paradigm of bounded rationality): ńćlovńõk - manaŇĺer d√°v√° pŇôednost variant√°m ŇôeŇ°en√≠, kter√© povaŇĺuje za "dosti dobr√©" pŇôed variantou optim√°ln√≠. V√Ĺbńõr ŇôeŇ°en√≠ nelze algoritmizovat, prov√°dńõt mechanicky. Prov√°d√≠ jej zpravidla s plnou individu√°ln√≠ odpovńõdnost√≠ manaŇĺer.
1.2.7. Anthonyho taxonomie manaŇĺersk√Ĺch aktivit
Kr√°tce po uveŇôejnńõn√≠ Simonovy klasifikace rozhodovac√≠ch procesŇĮ navrhl v r. 1965 R. N. Anthony rozdńõlen√≠ manaŇĺersk√Ĺch aktivit do tŇô√≠ oblast√≠, kter√© dobŇôe koresponduj√≠ se Simonovou klasifikac√≠:
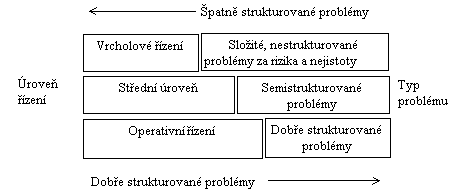
Obr√°zek 1.2 ‚ÄĚTypy rozhodovac√≠ch probl√©mŇĮ podle √ļrovn√≠ Ňô√≠zen√≠‚ÄĚ
Donnelly, J.H., Gibson, J.L., Ivancevich, J.M.: Management, Grada, Praha, 1997, str. 167.
Kontrolní otázky:
1. Charakterizujte rozdíl
mezi disciplinami Management Science a Operation Research.
2. TŇôi f√°ze rozhodovac√≠ho procesu podle
Simona: patŇô√≠ implementace do nńõkter√© z f√°z√≠?
3. Dok√°Ňĺete klasifikovat probl√©my ve vaŇ°em
Ňĺivotńõ jinak, neŇĺ to provedl Simon?
4. Korespondence typŇĮ rozhodov√°n√≠ s √ļrovnńõmi
manaŇĺersk√©ho Ňô√≠zen√≠ (dle Anthonyho) - odpov√≠d√° podle vaŇ°eho n√°zoru
bńõŇĺn√© praxi?
5. V oblastech
a) v√Ĺrobn√≠ z√°vod
e) letiŇ°tn√≠ provoz
b) zemńõdńõlsk√° farma
f) hotel
c) nemocnice
g) atomov√° elektr√°rna
d) banka
h) obchodn√≠ dŇĮm
formulujte pŇô√≠klady probl√©mŇĮ:
1.2.8. Obt√≠Ňĺnost rozhodov√°n√≠
Ve sloŇĺit√Ĺch rozhodovac√≠ch situac√≠ch (napŇô. v zemńõdńõlstv√≠), je obt√≠Ňĺnost rozhodov√°n√≠ zpŇĮsobena Ňôadou rŇĮzn√Ĺch faktorŇĮ:
Rozhodování probíhá za:
a) jistoty - o syst√©mu, v nńõmŇĺ rozhodujeme,
m√°me vŇ°echny potŇôebn√© informace;
b) rizika - dŇĮsledky naŇ°eho rozhodnut√≠
jsou z√°visl√© i na n√°hodn√Ĺch faktorech, jejichŇĺ rozdńõlen√≠ pravdńõpodobnost√≠
zn√°me;
c) nejistoty - nezn√°me pravdńõpodobnostn√≠
m√≠ry n√°hodn√Ĺch jevŇĮ ovlivŇąuj√≠c√≠ch prŇĮbńõh rozhodov√°n√≠.
1.2.10. PŇô√≠stupy k rozhodov√°n√≠
a) Subjektivn√≠ zaloŇĺen√© na:
b) Objektivn√≠ pŇô√≠stup (systematick√°
anal√Ĺza) pŇôedpokl√°d√°, Ňĺe se n√°vrhy vypracov√°vaj√≠ na z√°kladńõ anal√Ĺzy
dat o minul√©m dlouhodob√©m v√Ĺvoji syst√©mu.
Jde o rozbor soustavn√Ĺch z√°znamŇĮ o jevech, a
proto je cel√Ĺ postup velmi zdlouhav√Ĺ, pracn√Ĺ a ńćasovńõ n√°rońćn√Ĺ.
Nelze pŇôedem ovńõŇôit spr√°vnost n√°vrhu, a proto je zde znańćn√© riziko
omylu.
c) Vńõdeck√Ĺ pŇô√≠stup (objektivn√≠ a progresivn√≠) kombinuje oba pŇôedchoz√≠ postupy a vyuŇĺ√≠v√° metody modelov√°n√≠. Analyzuje a pozn√°v√° chov√°n√≠ syst√©mu pomoc√≠ umńõl√©ho syst√©mu - modelu, kter√Ĺ je obrazem re√°ln√©ho objektu.

Obr√°zek 1.3 ‚ÄĚPrincip vńõdeck√©ho pŇô√≠stupu k rozhodov√°n√≠‚ÄĚ
Na obr√°zku 1.3 je zobrazen postup pŇôi rozhodov√°n√≠ pomoc√≠ techniky modelov√°n√≠. Nejprve se vyslov√≠ hypot√©za o rozhodnut√≠ a jeho dŇĮsledc√≠ch. Ta se otestuje pomoc√≠ experimentu s matematick√Ĺm modelem. Na z√°kladńõ v√ĹsledkŇĮ experimentu se buńŹ povaŇĺuje za spr√°vnou a pouŇĺije se jako podklad pro rozhodnut√≠, nebo se oprav√≠ (resp. vytvoŇô√≠ nov√°) a znovu se otestuje.
Na obr√°zku 1.4 je uvedeno zapojen√≠ modelov√© techniky do procesu rozhodov√°n√≠. Podpora rozhodov√°n√≠ s vyuŇĺit√≠m matematick√Ĺch modelŇĮ je odborn√° a kvalifikovan√° ńćinnost, kter√° vyŇĺaduje t√Ĺmovou spolupr√°ci odborn√≠kŇĮ z rŇĮzn√Ĺch vńõdn√≠ch oblast√≠.

Obr√°zek 1.4 ‚ÄĚZapojen√≠ modelov√© techniky do //--> procesu rozhodov√°n√≠‚ÄĚ
Modelov√°n√≠ pŇôedstavuje proces zobrazov√°n√≠ a zkoum√°n√≠ jevŇĮ a syst√©mŇĮ pomoc√≠ modelŇĮ. Je to postup, pŇôi kter√©m jeden syst√©m (origin√°l) zobrazujeme jin√Ĺm syst√©mem (modelem). Matematick√© modelov√°n√≠ je formalizovan√Ĺ postup, pŇôi kter√©m origin√°l zobrazujeme a zkoum√°me pomoc√≠ modelu vytvoŇôen√©ho matematick√Ĺmi zobrazovac√≠mi prostŇôedky. Matematick√© modelov√°n√≠ se stalo obecn√Ĺm apar√°tem jednotliv√Ĺch vńõdn√≠ch discipl√≠n. Syst√©mov√© modelov√°n√≠ je matematick√© modelov√°n√≠ vybudovan√© na syst√©mov√Ĺch principech.
1.2.11. Efektivnost a √ļńćinnost podpory rozhodov√°n√≠
Kvalitu rozhodov√°n√≠ pŇôi Ňô√≠zen√≠ syst√©mu mŇĮŇĺeme hodnotit z hlediska dvou aspektŇĮ: efektivnosti a √ļńćinnosti (effectiveness and efficiency). Efektivnost Ňô√≠zen√≠ syst√©mu vyjadŇôuje stupeŇą dosaŇĺen√≠ c√≠lŇĮ - je tedy vyj√°dŇôena ohodnocen√≠m v√ĹstupŇĮ. √öńćinnost Ňô√≠zen√≠ lze vyj√°dŇôit mnoŇĺstv√≠m spotŇôebovan√Ĺch vstupŇĮ, zdrojŇĮ.
Efektivnost rozhodov√°n√≠ je tedy m√≠rou dosaŇĺen√©ho v√Ĺstupu, √ļńćinnost rozhodov√°n√≠ je m√≠rou vyuŇĺit√≠ vstupŇĮ. Syst√©m mŇĮŇĺe b√Ĺt z hlediska Ňô√≠zen√≠ velmi efektivn√≠, ale √ļńćinnost jeho Ňô√≠zen√≠ n√≠zk√°, pokud pro dosaŇĺen√≠ c√≠lŇĮ je tŇôeba vynaloŇĺit enormn√≠ n√°klady.
Metody MS/OR maj√≠ svoji podporou vliv na efektivnost √ļńćinnosti Ňô√≠zen√≠ syst√©mu.
1.2.12. VyuŇĺ√≠v√°n√≠ kvantitativn√≠ch metod pŇôi podpoŇôe rozhodov√°n√≠
Kvantitativn√≠ metody jsou vyuŇĺ√≠v√°ny jako podpora
rozhodování (Decision Support Systems - Systémy pro podporu rozhodování).
Tyto metody samy o sobńõ rozhodovac√≠ probl√©my nevyŇôeŇ°√≠. UŇĺiteńćnost
kvantitativn√≠ch metod podle prŇĮzkumu u americk√Ĺch firem vypl√Ĺv√° z
tabulky 1.2.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tabulka 1.2 ‚ÄĚUŇĺiteńćnost kvantitativn√≠ch metod‚ÄĚ
Z tabulky je patrn√©, Ňĺe v√≠ce neŇĺ 90%
firem uv√°d√≠ uŇĺiteńćnost tńõchto metod a pouze necel√Ĺch 10% se domn√≠v√°,
Ňĺe jejich uŇĺiteńćnost je mal√°. V tabulce 1.3 je uveden pŇôehled pouŇĺit√≠
rŇĮzn√Ĺch matematick√Ĺch modelŇĮ v urńćit√©m typu rozhodovac√≠ho prostŇôed√≠.
|
|
|
|
|
|
|
|
spolehlivost |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
||||||
|
|
|
|
|
|
||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
Tabulka 1.3 ‚ÄĚPouŇĺit√≠ matematick√Ĺch modelŇĮ v urńćit√©m typu rozhodovac√≠ho prostŇôed√≠‚ÄĚ
Kontrolní otázky:
10. Rozhodnńõte, kter√© z rozhodovac√≠ch situac√≠ prob√≠haj√≠ za jistoty, rizika, nejistoty:
1.3.1. Definice
Model je z√°mńõrnńõ zjednoduŇ°en√Ĺ obraz reality.
1.3.2. Klasifikace modelŇĮ
Reprezentace nebo abstrakce reality pomoc√≠ modelu pŇôedpokl√°d√° pouŇĺit√≠ vhodn√Ĺch zobrazovac√≠ch prostŇôedkŇĮ. Podle typu zobrazen√≠ reality do modelu rozliŇ°ujeme tŇôi z√°kladn√≠ typy modelŇĮ:
1) Modely ikonick√©. Jedn√° se o fyzik√°ln√≠ repliky re√°ln√©ho syst√©mu (pŇôedmńõtu). Jsou pŇôesn√©, nebo zjednoduŇ°en√©, ve zmenŇ°en√©m, nebo zvńõtŇ°en√©m mńõŇô√≠tku. PŇô√≠klady: modely strojŇĮ, repliky historick√Ĺch automobilŇĮ, modely staveb, model atomu.
2) Modely analogick√©. Jedn√° se o mechanick√© a elektronick√© analogy syst√©mŇĮ. PŇô√≠klady: pl√°ny mńõst, mapy, pl√°ny inŇĺen√Ĺrsk√Ĺch s√≠t√≠, analogov√Ĺ model Steiner-Weberovy √ļlohy chemick√© vzorce.
3) Modely matematické. Soustavy funkcí,
soustavy rovnic, soustavy funkcion√°lŇĮ. Matice a grafy. Speci√°ln√≠ programy
pońć√≠tańćŇĮ. PŇô√≠klady: Rovnice speci√°ln√≠ teorie relativity. Vzorec
pro v√Ĺpońćet rychlosti voln√©ho p√°du tńõlesa ve vakuu. Model zemńõdńõlsk√©
v√Ĺroby farmy pomoc√≠ line√°rn√≠ho programov√°n√≠. S√≠Ň•ov√Ĺ model syst√©mu
n√°vazn√Ĺch procesŇĮ. Simulace syst√©mu hromadn√© obsluhy. Program pro
Ňô√≠zen√≠ manipul√°toru.
V MS se pouŇĺ√≠vaj√≠ v√Ĺhradnńõ matematick√©
modely.
1.3.3. Z√°kladn√≠ sloŇĺky matematick√©ho modelu
V kaŇĺd√©m matematick√©m modelu mŇĮŇĺeme rozliŇ°it tŇôi z√°kladn√≠ skupiny objektŇĮ, ze kter√Ĺch se model skl√°d√°. Jsou to
1. promńõnn√© a konstanty,
2. matematické struktury,
3. ŇôeŇ°en√≠.
1.3.4. Promńõnn√© a konstanty v matematick√©m modelu
1. Promńõnn√© a konstanty identifikovan√© (pojmenovan√©).
Identifikovan√° promńõnn√° nebo konstanta pŇôedstavuje konkr√©tn√≠ vlastnost
re√°ln√©ho objektu, coŇĺ se projevuje n√°zvem a m√≠rou. PŇô√≠klady:
xk je v√Ĺmńõra pŇ°enice ozim√© v ha, xr produkce
pŇ°enice ozim√© v katastru ‚ÄúU kŇô√≠Ňĺku‚ÄĚ v t, ![]() n√°hodn√° doba ńćek√°n√≠ sedm√© jednotky v syst√©mu hromadn√© obsluhy v
pátém kanálu obsluhy v minutách, cik vzdálenost
dodavatele Di od spotŇôebitele Sk
v
km.
n√°hodn√° doba ńćek√°n√≠ sedm√© jednotky v syst√©mu hromadn√© obsluhy v
pátém kanálu obsluhy v minutách, cik vzdálenost
dodavatele Di od spotŇôebitele Sk
v
km.
2. Promńõnn√© a konstanty neidentifikovan√© (pomocn√©).SlouŇĺ√≠ pro formalizaci matematick√©ho z√°pisu, chod algoritmŇĮ apod.
3. Rozhodovac√≠ promńõnn√©. PŇôedstavuj√≠
zpravidla nejdŇĮleŇĺitńõjŇ°√≠ procesy modelovan√©ho syst√©mu, kter√© se
v matematick√©m modelov√°n√≠ naz√Ĺvaj√≠ aktivity nebo entity nebo rozhodovac√≠
promńõnn√©. PŇô√≠klady: v modelu optimalizace portfolia promńõnn√© x1,
..., xn pŇôedstavuj√≠ pońćty akci√≠ podnikŇĮ P1, ...,
Pn . V modelu I =![]() pŇôedstavuj√≠ U a R aktivity a odpor v pŇô√≠sluŇ°n√Ĺch jednotk√°ch. Tńõmito
dvńõma aktivitami je urńćen proud. V syst√©mu hromadn√© obsluhy napŇô.
jednotka tj pŇôedstavuje se sv√Ĺmi charakteristikami tjk,
tjn entitu.
pŇôedstavuj√≠ U a R aktivity a odpor v pŇô√≠sluŇ°n√Ĺch jednotk√°ch. Tńõmito
dvńõma aktivitami je urńćen proud. V syst√©mu hromadn√© obsluhy napŇô.
jednotka tj pŇôedstavuje se sv√Ĺmi charakteristikami tjk,
tjn entitu.
4. Vstupn√≠ promńõnn√© a konstanty, v√Ĺstupn√≠ promńõnn√© a konstanty (endogenn√≠ a exogenn√≠ promńõnn√© a konstanty).
5. Nekontrolovateln√© promńõnn√© a konstanty.PŇôedstavuj√≠ procesy, jejichŇĺ m√≠ry nelze zjistit. PŇô√≠klady: Velikost m√≠ry inflace v chaotick√Ĺch a nestandardn√≠ch podm√≠nk√°ch nelze popsat ani pomoc√≠ pravdńõpodobnosti ani pomoc√≠ fuzzy m√≠ry. V modelech situac√≠ ‚Äúad hoc‚ÄĚ jsou charakteristiky pońćas√≠ nekontrolovateln√© konstanty nebo promńõnn√©, protoŇĺe nelze vyuŇĺ√≠t pońćtu pravdńõpodobnosti pro jejich popis.
6. V√Ĺsledn√© promńõnn√© a konstanty. Ud√°vaj√≠ hodnoty ŇôeŇ°en√≠, popisuj√≠ v√Ĺslednou informaci.
1.3.5. Matematické struktury (omezující podmínky) v matematickém modelu
V ekonomicko matematick√Ĺch modelech se matematick√© struktury naz√Ĺvaj√≠ omezuj√≠c√≠ podm√≠nky. Dńõl√≠me je podle pouŇĺit√©ho matematick√©ho apar√°tu z nńõkter√©ho odvńõtv√≠ matematiky:
1) Analytick√© struktury. Jedn√° se o objekty z odvńõtv√≠ Matematick√© anal√Ĺzy, Line√°rn√≠ algebry a dalŇ°√≠ch odvńõtv√≠ matematiky. PŇô√≠klad: soustavy rovnic (line√°rn√≠, neline√°rn√≠, skal√°rn√≠, vektorov√©, diferenci√°ln√≠, integr√°ln√≠, maticov√©, atd.), soustavy nerovnic (line√°rn√≠, neline√°rn√≠, se sm√≠Ň°en√Ĺmi omezen√≠mi, atd.), funkce (element√°rn√≠, sloŇĺen√©, holomorfn√≠, stochastick√©, fuzzy, atd.), funkcion√°ly, atd.
2) Geometrick√© struktury. Model je pops√°n grafick√Ĺmi prostŇôedky: body, pŇô√≠mkami, rovinami, kŇôivkami. PŇô√≠klad: Geometrick√° interpretace a ŇôeŇ°en√≠ √ļloh v modelech line√°rn√≠ho programov√°n√≠. Grafick√° interpretace rovnov√°hy nab√≠dky a popt√°vky v ekonometrick√Ĺch modelech, atd.
3) Topologick√© struktury. Modely jsou vytv√°Ňôeny pomoc√≠ objektŇĮ matematick√© teorie grafu. PŇô√≠klad: Modely maxim√°ln√≠ch tokŇĮ v s√≠t√≠ch, nejspolehlivńõjŇ°√≠ cesty v grafu/s√≠ti. Dopravn√≠ a distribuńćn√≠ syst√©my zobrazen√© grafem. Logistick√© syst√©my popsan√© pomoc√≠ grafŇĮ a sch√©mat. Topologick√© modely lze zpravidla ekvivalentnńõ zobrazovat pomoc√≠ tzv. incidenńćn√≠ch matic (tabulek, matic souslednosti, apod.).
4) Artefici√°ln√≠ struktury. Modely jsou pops√°ny prvky programovac√≠ho jazyka. PŇô√≠klad: Model syst√©mu z√°sob popsan√Ĺ v√Ĺvojov√Ĺm diagramem (simulańćn√≠m jazykem SIMULA 67, objektovńõ orientovan√Ĺm jazykem Smalltalk, atd.).
5) Kvalitativn√≠ struktury. Model je pops√°n pomoc√≠ kvalitativn√≠ch rovnic, kvalitativn√≠ch nerovnost√≠ nebo v√°gnńõ. PŇô√≠klad: kvalitativn√≠ matice, kvalitativn√≠ graf, jazykov√Ĺ oper√°tor "velmi" v teorii fuzzy mnoŇĺin, atd.
Nńõkter√© speci√°ln√≠ a pŇôedevŇ°√≠m jiŇĺ standardn√≠ struktury matematick√©ho modelu maj√≠ specifick√© n√°zvy. PŇô√≠klady: Cobb-Douglasova funkce. √öńćelov√° funkce. Podm√≠nky nez√°pornosti. Lagreangova funkce. Wolfeho podm√≠nky.
1.3.6. ŇėeŇ°en√≠ matematick√©ho modelu
ŇėeŇ°en√≠ modelu klasifikujeme podle hlediska c√≠lŇĮ modelov√°n√≠:
1) PŇô√≠pustn√© ŇôeŇ°en√≠, nepŇô√≠pustn√© ŇôeŇ°en√≠ - ŇôeŇ°en√≠ vyhovuje, ŇôeŇ°en√≠ nevyhovuje omezuj√≠c√≠m podm√≠nk√°m.
2) Maxim√°ln√≠ ŇôeŇ°en√≠, minim√°ln√≠ ŇôeŇ°en√≠ - ŇôeŇ°en√≠ splŇąuje maximalizańćn√≠ nebo minimalizańćn√≠ c√≠lovou podm√≠nku.
3) Optim√°ln√≠ ŇôeŇ°en√≠ - ŇôeŇ°en√≠ vyhovuje nejl√©pe poŇĺadovan√©mu c√≠li podle pŇôedstav a poŇĺadavkŇĮ manaŇĺera (tj. nemus√≠ b√Ĺt nutnńõ maxim√°ln√≠ ńći minim√°ln√≠).
4) V√Ĺchoz√≠ ŇôeŇ°en√≠ - ŇôeŇ°en√≠ zpravidla zadan√© odhadem nebo sestrojen√© vhodn√Ĺm jednoduch√Ĺm algoritmem. Nen√≠ optim√°ln√≠, pouŇĺ√≠v√° se jako start v algoritmech typu ‚Äústep by step‚ÄĚ, kter√© jsou zaloŇĺeny na postupn√©m zlepŇ°ov√°n√≠ v√Ĺchoz√≠ho ŇôeŇ°en√≠ aŇĺ do jeho optim√°ln√≠ho tvaru.
5) V√Ĺsledn√© ŇôeŇ°en√≠ - ŇôeŇ°en√≠, kter√© mŇĮŇĺe b√Ĺt vybr√°no jako optim√°ln√≠. V√Ĺsledn√Ĺch ŇôeŇ°en√≠ mŇĮŇĺe b√Ĺt k disposici koneńćnńõ nebo i nekoneńćnńõ mnoho. Z mnoŇĺiny v√Ĺsledn√Ĺch ŇôeŇ°en√≠ (alternativ) vyb√≠r√° manaŇĺer ŇôeŇ°en√≠ pro praxi nejvhodnńõjŇ°√≠ (optim√°ln√≠).
6) Alternativn√≠ ŇôeŇ°en√≠ - ŇôeŇ°en√≠, kter√© je podle pŇôedem zadan√Ĺch kriteri√≠ rovnocen√© s jin√Ĺm ŇôeŇ°en√≠m. PŇô√≠klad: Dvńõ strategie investic do vybaven√≠ podniku pŇôedpokl√°daj√≠ sice rŇĮzn√© technologie, ale garantuj√≠ dosaŇĺen√≠ stejn√© v√ĹŇ°e zisku.
7) Aproximativn√≠ ŇôeŇ°en√≠ - ŇôeŇ°en√≠ vyhovuje omezuj√≠c√≠m podm√≠nk√°m pŇôibliŇĺnńõ nebo se k c√≠li pouze pŇôibliŇĺuje (zpravidla se poŇĺaduje, aby term√≠n "pŇôibliŇĺnńõ" byl vhodn√Ĺm zpŇĮsobem determinov√°n, napŇô. byla zn√°ma v√ĹŇ°e ztr√°ty, kdyŇĺ ŇôeŇ°en√≠ pouŇĺijeme).
1.3.7. Klasifikace matematick√Ĺch modelŇĮ
Matematick√© modely se pouŇĺ√≠vaj√≠ prakticky ve
vŇ°ech vńõd√°ch a rozvoj jednotliv√Ĺch vńõd je na jejich vyuŇĺ√≠v√°n√≠
bezprostŇôednńõ z√°visl√Ĺ. StupeŇą matematizace vńõdn√≠ho oboru je uzn√°van√Ĺm
mńõŇô√≠tkem jeho kvality a z√°rukou rozvoje. V oblastech pŇô√≠rodn√≠ch
a fyzik√°ln√≠ch vńõd, technice, ekonomii, managementu, marketingu, soci√°ln√≠ch
a spoleńćensk√Ĺch vńõd√°ch se pouŇĺ√≠v√° velk√© mnoŇĺstv√≠ rŇĮzn√Ĺch typŇĮ
matematick√Ĺch modelŇĮ, kter√© mŇĮŇĺeme klasifikovat podle rŇĮzn√Ĺch hledisek.
NejobecnńõjŇ°√≠ klasifikace dńõl√≠ matematick√© modely do dvou skupin:
1. Modely deskriptivní.
2. Modely normativní.
1.3.8. Modely deskriptivní
SlouŇĺ√≠ k zobrazen√≠ prvkŇĮ a vztahŇĮ v syst√©mu a k anal√Ĺze z√°kladn√≠ch vlastnost√≠ syst√©mu. Nezaj√≠m√° n√°s urńćit√© c√≠lov√© chov√°n√≠ syst√©mu, pouze syst√©m s√°m o sobńõ. Pomoc√≠ tńõchto typŇĮ modelŇĮ se odvozuj√≠ dalŇ°√≠ vlastnosti syst√©mu, urńćuje se jeho rovnov√°Ňĺn√Ĺ stav, stabiln√≠ stav, vliv zmńõn uvnitŇô i ve vnńõjŇ°√≠m okol√≠ syst√©mu na jeho chov√°n√≠. PŇô√≠klady: Rovnice E = mc2 , ekonometrick√Ĺ meziodvńõtvov√Ĺ model "Imput-Output", soustava diferenci√°ln√≠ch rovnic modeluj√≠c√≠ procesy zrodu a √ļmrt√≠, simulańćn√≠ model modeluj√≠c√≠ v√Ĺskyt Ň°kŇĮdcŇĮ porostu, rovnice nab√≠dky a popt√°vky v konkurenńćn√≠m prostŇôed√≠.
1.3.9. Modely normativní
SlouŇĺ√≠ k anal√Ĺze a Ňô√≠zen√≠ syst√©mu tak, aby byl splnńõn nńõjak√Ĺ c√≠l nebo mnoŇĺina c√≠lŇĮ. Zaj√≠m√° n√°s c√≠lov√© chov√°n√≠ syst√©mu. Normativn√≠ model b√Ĺv√° ńćasto doplnńõn tzv. c√≠lovou (√ļńćelovou) funkc√≠ nebo soustavou takov√Ĺch funkc√≠. Nutnou souńć√°st√≠ normativn√≠ho modelu je extrem√°ln√≠ (minim√°ln√≠/maxim√°ln√≠) ŇôeŇ°en√≠, kter√© d√°v√° n√°vod, jak poŇĺadovan√©ho c√≠le (resp. c√≠lŇĮ) dos√°hnout. Normativn√≠ modely, jejichŇĺ c√≠lem je nalezen√≠ optim√°ln√≠ho ŇôeŇ°en√≠, se naz√Ĺvaj√≠ optimalizańćn√≠ modely.
1.3.10. Klasifikace normativn√≠ch a deskriptivn√≠ch modelŇĮ
Modely deskriptivn√≠ i normativn√≠ jsou d√°le dńõleny podle typu syst√©mu, k jehoŇĺ modelov√°n√≠ slouŇĺ√≠, nebo podle typu matematick√Ĺch sloŇĺek (promńõnn√©, struktury, ŇôeŇ°en√≠) jeŇĺ obsahuj√≠.
1) Modely statick√©. Model zobrazuje a analyzuje syst√©m bez zŇôetele k jeho ńćasov√©mu v√Ĺvoji. Zobrazen√≠ se t√Ĺk√° zpravidla urńćit√©ho ńćasov√©ho intervalu (t√Ĺden, mńõs√≠c, rok, apod.).
2) Modely dynamick√©. Model zobrazuje a analyzuje syst√©m v prŇĮbńõhu ńćasu. Zobrazen√≠ mŇĮŇĺe b√Ĺt typu ‚Äúex post‚ÄĚ nebo ‚Äúex ante‚ÄĚ a respektovat kr√°tk√Ĺ ńći delŇ°√≠ ńćasov√Ĺ horizont.
3) Modely dynamizovan√©. Zpravidla se jedn√° o vyj√°dŇôen√≠ ńćasov√©ho prvku ve statick√©m modelu pomoc√≠ speci√°ln√≠ch modelov√Ĺch technik. Dynamizovan√© modely se pouŇĺ√≠vaj√≠ v pŇô√≠padńõ, kdy odpov√≠daj√≠c√≠ dynamick√Ĺ model je velmi sloŇĺit√Ĺ nebo jej nedovedeme soudob√Ĺmi modelov√Ĺmi technikami spolehlivńõ konstruovat.
4) Modely deterministick√©. VŇ°echny promńõnn√©, konstanty a funkce v modelu jsou deterministick√© (nen√°hodn√©) velińćiny nebo funkce.
5) Modely stochastick√©. AlespoŇą jedna promńõnn√°, konstanta nebo funkce v modelu je n√°hodn√° velińćina nebo n√°hodn√° funkce.
6) Fuzzy modely. Nńõkter√© promńõnn√©, konstanty nebo funkce jsou fuzzy velińćiny, nebo fuzzy funkce.
V MS se pouŇĺ√≠vaj√≠ vŇ°echny uveden√© typy modelŇĮ. Modely normativn√≠ pŇôevaŇĺuj√≠ v oblasti operativn√≠ho Ňô√≠zen√≠, modely deskriptivn√≠ jsou nejńćastńõji pouŇĺ√≠v√°ny v oblasti vrcholov√©ho managementu - strategick√©m pl√°nov√°n√≠. Modely statick√©, dynamick√©, deterministick√© a stochastick√© se pouŇĺ√≠vaj√≠ ve vŇ°ech oblastech managementu. Podle povahy probl√©mu se modely v MS pouŇĺ√≠vaj√≠ individu√°lnńõ nebo v kombinac√≠ch. Pro ŇôeŇ°en√≠ zn√°m√Ĺch probl√©mŇĮ lze pouŇĺ√≠t tzv. standardn√≠ modely. Pro ŇôeŇ°en√≠ nov√Ĺch probl√©mŇĮ je tŇôeba konstruovat nov√© modely.
1.3.11. Modelování nejistoty a rizika
Nejistotou pŇôi zobrazen√≠ syst√©mu pomoc√≠ matematick√©ho modelu rozum√≠me situaci, kdy nem√°me k disposici vŇ°echnu potŇôebnou informaci nebo kdy nńõkter√© z informac√≠ jsou nespolehliv√©.
Modelov√°n√≠ pŇôi riziku pŇôedpokl√°d√°, Ňĺe nńõkter√© informace jsou n√°hodn√© velińćiny, nebo Ňĺe nńõkter√© procesy jsou pops√°ny n√°hodn√Ĺmi funkcemi. V pŇô√≠padńõ modelŇĮ s rizikem mŇĮŇĺeme velikost rizika pŇôi pŇôijet√≠ ŇôeŇ°en√≠ popsat pomoc√≠ pravdńõpodobnostn√≠ch charakteristik.
Analogicky mŇĮŇĺeme povaŇĺovat modelov√°n√≠ za rizika i v pŇô√≠padńõ pouŇĺit√≠ fuzzy velińćin, nebo fuzzy funkc√≠. Velikost rizika lze potom vyj√°dŇôit buńŹ pomoc√≠ vhodn√© fuzzy m√≠ry nebo tuto fuzzy m√≠ru transformovat na subjektivn√≠ pravdńõpodobnost.
1.3.12. Sedm v√Ĺhod matematick√©ho modelu (‚ÄúSedm S matematick√©ho modelu‚ÄĚ)
1) √öspora ńćasu. Operace prob√≠haj√≠c√≠ v re√°ln√©m ńćase po l√©ta mohou b√Ĺt simulov√°ny pomoc√≠ modelu bńõhem nńõkolika minut (Simulace).
2) JednoduŇ°Ň°√≠ manipulace s modelem neŇĺ s realitou (Simplicita).
3) Cena za chybn√© rozhodnut√≠ pŇôi pr√°ci s modelem je nepatrn√° ve srovn√°n√≠ s chybou v re√°ln√©m syst√©mu (Spolehlivost).
4) MoŇĺnost kalkulace rizika spojen√©ho s pŇôijet√≠m rozhodnut√≠ (Stabilita).
5) Cena za anal√Ĺzu chov√°n√≠ syst√©mu pomoc√≠ modelu je mnohem menŇ°√≠ neŇĺ cena za anal√Ĺzu re√°ln√©ho syst√©mu (SpoŇôivost).
6) Modelov√°n√≠m se uŇĺivatel uńć√≠ (Sebevzdńõl√°v√°n√≠).
7) MoŇĺnost anal√Ĺzy a posouzen√≠ velk√©ho mnoŇĺstv√≠ (i nekoneńćn√©ho pońćtu) alternativ ŇôeŇ°en√≠ (Selektivita).
1.3.13. Standardní matematické modely
Metody MS se rozv√≠jej√≠ od r. 1945. Za pomńõrnńõ dlouhou dobu jejich existence bylo provedeno mnoho aplikac√≠, nńõkter√© z nich jsou dnes povaŇĺov√°ny za standardn√≠. KaŇĺd√° standardn√≠ metoda odpov√≠d√° urńćit√Ĺm typŇĮm manaŇĺersk√Ĺch probl√©mŇĮ. N√°sleduj√≠c√≠ pŇôehled uv√°d√≠ velmi zjednoduŇ°en√Ĺ pŇôehled manaŇĺersk√Ĺch probl√©mŇĮ a matematick√Ĺch modelŇĮ
1.3.14. PŇôehled standardn√≠ch manaŇĺersk√Ĺch probl√©mŇĮ ŇôeŇ°en√Ĺch s podporou Management Science
a) Alokańćn√≠ probl√©my (Allocation problems). Jedn√° se o situace, kdy (i) je tŇôeba splnit urńćit√© aktivity, (ii) existuje v√≠ce rŇĮzn√Ĺch zpŇĮsobŇĮ, jak tyto aktivity splnit, (iii) zdroje a v√Ĺrobn√≠ postupy jsou omezeny. C√≠lem je nejlepŇ°√≠ vyuŇĺit√≠ zdrojŇĮ.
b) Chov√°n√≠ v konkurenńćn√≠m prostŇôed√≠ (Competitive situations). Situace podobn√° hŇôe, v n√≠Ňĺ se kaŇĺd√° strana snaŇĺ√≠ zv√≠tńõzit.
c) Distribuńćn√≠ probl√©my (Distribution problems). Rozm√≠stńõn√≠ zdrojŇĮ, objektŇĮ. PŇôiŇôazen√≠ pracovn√≠kŇĮ. Dopravn√≠ probl√©my.
d) Z√°soby a sklady (Inventory control). Stanoven√≠ v√ĹŇ°e z√°sob, finanńćn√≠ch a lidsk√Ĺch zdrojŇĮ v podniku v kr√°tkodob√©m i dlouhodob√©m ńćasov√©m horizontu.
e) Progn√≥zov√°n√≠, pŇôedv√≠d√°n√≠, pl√°nov√°n√≠ (Predicting the behaviour of a system). Popis budouc√≠ho v√Ĺvoje syst√©mu pŇôi respektov√°n√≠ ońćek√°van√Ĺch zmńõn uvnitŇô i vnńõ syst√©mu.
f) S√≠Ň•ov√© probl√©my a logistick√© Ňô√≠zen√≠ (Network problems). Ňė√≠zen√≠ tokŇĮ komodit, zdrojŇĮ, financ√≠, informac√≠ mezi v√Ĺrobn√≠mi a spoleńćensk√Ĺmi objekty.
g) Probl√©my front (Waiting line problems). Syst√©mu hromadn√© obsluhy. Ňė√≠zen√≠ syst√©mu s ńćek√°n√≠m, frontami, obsluhou klientŇĮ. Organizace sluŇĺeb, v√Ĺrobn√≠ch operac√≠, obchodn√≠ch ńćinnost√≠, oprav√°renstv√≠, servisy, letiŇ°tńõ, apod.
h) √ödrŇĺba, obnova a spolehlivost (Maintenance, renewal, reliability). Strategie √ļdrŇĺby, obnovy a spolehlivost u v√Ĺrobn√≠ch i veŇôejnńõ pr√°vn√≠ch zaŇô√≠zen√≠. Ňė√≠zen√≠ investic. Organizace kapit√°lov√©ho trhu.
i) Person√°ln√≠ Ňô√≠zen√≠ (Personal Management). V√Ĺbńõr a provńõŇôov√°n√≠ pracovn√≠kŇĮ. Syst√©mov√° anal√Ĺza kvalifikańćn√≠ch zdrojŇĮ. Permanentn√≠ vzdńõl√°v√°n√≠ a proŇ°kolov√°n√≠.
j) Ňė√≠zen√≠ administrativy(Administrative Control). Optimalizace m√≠stn√≠, region√°ln√≠, st√°tn√≠ spr√°vy. Ňė√≠zen√≠ podnikov√© administrativy.
1.3.15. PŇôehled standardn√≠ch matematick√Ĺch modelŇĮ a modelov√Ĺch technik
a) Matematické programování (Mathematical programming).
b) Dynamické programování (Dynamic programming).
c) Modely hromadné obsluhy (Waiting/queuing
models).
d) Modely z√°sob (Inventory models).
e) Modely obnovy (Renewal models).
f) Markovovy Ňôetńõzce (Markov chains).
g) S√≠Ň•ov√© modely (Network models).
h) Heuristické/Stochastické programování
(Heuristic/Stochastic programming).
i) Simulańćn√≠ modely (Simulation models).
j) Metody vńõtv√≠ a hranic (Branch and bound).
k) Rozhodovací modely (Decision models, Decision
tables/trees )
l) Modely teorie her (Game theory).
m) Systémy pro podporu rozhodování (Decision
support systems).
n) Expertní systémy (Expert systems).
VŇ°echny standardn√≠ matematick√© modely
jsou ŇôeŇ°iteln√© pomoc√≠ software, kter√Ĺ je k disposici na trhu pro rŇĮzn√©
√ļrovnńõ pouŇĺit√≠ - od pedagogick√Ĺch (Ň°koln√≠ch) programŇĮ aŇĺ po vysoce
profesion√°ln√≠ programy. Mezi nejzn√°mńõjŇ°√≠ produkty patŇô√≠ LINDO (ve
verz√≠ch LINGO, What¬īs the best), QSB. Mnoho √ļloh lze ŇôeŇ°it v produktech
MS-Excel, SAS, Maple, aj.
1900 1910 1920 1930 1940 1950
1960 1970 1980 1990 2000
Obr√°zek 1.5 ‚ÄĚHistorick√Ĺ v√Ĺvoj matematick√Ĺch
modelŇĮ pouŇĺ√≠van√Ĺch v MS‚ÄĚ
(Adaptov√°no podle: Turban E.,
Meredith R.J.: Fundamentals of Management Science)
1.4. Systémové modelování
Metodologie modelov√°n√≠ se rozv√≠j√≠ v r√°mci samostatn√© odborn√© specializace ‚ÄúTeorie modelov√°n√≠‚ÄĚ, kter√° je souńć√°st√≠ syst√©mov√© vńõdy. Vysvńõtl√≠me nńõkter√© pojmy teorie syst√©mov√©ho modelov√°n√≠.
1.4.1. Systémové modelování
Postup pŇôi syst√©mov√©m modelov√°n√≠ re√°ln√©ho syst√©mu je uveden na obr√°zku 1.6. Jde o permanentn√≠ interaktivn√≠ proces s ńćetn√Ĺmi zpńõtn√Ĺmi vazbami, kter√Ĺ se nńõkolikr√°t opakuje.
1) Formulace probl√©mu. Spr√°vn√° formulace probl√©mu je velmi dŇĮleŇĺit√° pro dalŇ°√≠ postup ŇôeŇ°en√≠. Je tŇôeba vyj√≠t z diagnostiky pot√≠Ňĺ√≠ syst√©mu, z celkov√© jeho anal√Ĺzy a stanoven√Ĺch c√≠lŇĮ.
2) Zaveden√≠ syst√©mu. Realita je sloŇĺit√°, je tŇôeba ji vymezit a pro √ļńćely modelu zjednoduŇ°it. Proto definujeme na realitńõ syst√©m, tj. prvky, vazby, vstupy a v√Ĺstupy, funkci. Jde o proces simplifikace (zjednoduŇ°en√≠) probl√©mu, kdy nepodstatn√© oddńõlujeme od podstatn√©ho.
3) Konstrukce modelu. Pro konstrukci modelu je rozhoduj√≠c√≠ √ļńćel, kter√Ĺ sledujeme. Ten rozhoduje o tom, co budeme v ekonomick√© skuteńćnosti pokl√°dat za v√Ĺznamn√© a co zahrneme do modelu a co jako podruŇĺn√© ponech√°me mimo model a mimo naŇ°e √ļvahy. Tvorba modelŇĮ patŇô√≠ k tvŇĮrńć√≠ ńćinnosti a vyjadŇôuje kromńõ dobr√© znalosti modelov√© techniky tak√© dobrou znalost vńõcn√© problematiky. KaŇĺd√Ĺ model mus√≠ vych√°zet z konkr√©tn√≠ hypot√©zy odvozen√© ze skuteńćnosti.

Obr√°zek 1.6 ‚ÄĚPostup modelov√°n√≠ syst√©mu‚ÄĚ
5) Kvantifikace modelu. Je naplnńõn√≠ modelu konkr√©tn√≠mi √ļdaji a daty. Je tŇôeba db√°t na jejich hodnovńõrnost.
6) V√Ĺpońćet modelu. Existuj√≠ dva zpŇĮsoby odvozen√≠ ŇôeŇ°en√≠ z modelu:
8) Synt√©za poznatkŇĮ. Shrnut√≠ z√≠skan√Ĺch poznatkŇĮ vńćetnńõ vŇ°ech aspektŇĮ, kter√© nebyly do matematick√©ho modelu zahrnuty.
9) Implementace. Implementace je volba postupu aplikace vybran√©ho ŇôeŇ°en√≠ v praxi.
1.4.2.Pozn√°mka
Modelov√° technika umoŇĺŇąuje experimentov√°n√≠ s modelem, tj. sledov√°n√≠ √ļńćinkŇĮ zmńõn jednotliv√Ĺch parametrŇĮ v modelu na v√Ĺsledn√© chov√°n√≠ syst√©mu a tak zjiŇ°Ň•ovat vliv rŇĮzn√Ĺch rozhodnut√≠ a z√°sahŇĮ rozhodovatele na fungov√°n√≠ syst√©mu. Vlastnosti reality tedy pozn√°v√°me pomoc√≠ experimentŇĮ s jej√≠m adekv√°tn√≠m zobrazen√≠m pomoc√≠ modelu. Toto experimentov√°n√≠ m√° povahu procesu uńćen√≠.
1.4.3. Obecné zásady systémového modelování
Podpora rozhodov√°n√≠ s vyuŇĺit√≠m matematick√©ho modelu je odborn√° a kvalifikovan√° ńćinnost, vyŇĺaduj√≠c√≠ t√Ĺmovou spolupr√°ci odborn√≠kŇĮ z rŇĮzn√Ĺch oblast√≠: odborn√≠ka z oblasti oboru ŇôeŇ°en√© problematiky, specialistu v oblasti MS, specialistu z oblasti informatiky, apod.
Metodologie syst√©mov√©ho modelov√°n√≠ se vyv√≠j√≠ jako samostatn√° odborn√° specializace, kter√° se v souńćasn√© dobńõ zaŇôazuje do Teorie syst√©mŇĮ jako souńć√°st tzv. Syst√©mov√© anal√Ĺzy. Obecn√© z√°sady, kter√© je tŇôeba pŇôi matematick√©m modelov√°n√≠ syst√©mŇĮ respektovat, lze velmi zjednoduŇ°enńõ popsat n√°sleduj√≠c√≠mi kroky:
1. Identifikace problému z hlediska matematického modelování.
7. Implementace.
1.4.4. PŇôedpoklady √ļspńõŇ°n√©ho modelov√°n√≠Monitoring implementace. Sledov√°n√≠ zpńõtn√© vazby. √öpravy modelu a nov√° implementace.
1) Znalost metod a prostŇôedkŇĮ ekonomick√© anal√Ĺzy. Je dŇĮleŇĺit√° pŇôi volbńõ spr√°vn√© metody a modelu.
2) Znalost techniky modelov√°n√≠. √ösil√≠ vynaloŇĺen√© na konstrukci a vyuŇĺit√≠ urńćit√©ho modelu mus√≠ b√Ĺt √ļmńõrn√© jeho pŇô√≠nosu.
3) Existuj√≠c√≠ syst√©m Ňô√≠zen√≠. Pracovn√≠ci praxe mus√≠ m√≠t dostateńćn√Ĺ prostor pro vlastn√≠ rozhodov√°n√≠ (iniciativa) a mus√≠ b√Ĺt hmotnńõ zainteresov√°ni na vyuŇĺit√≠ modelov√© techniky (motivace).
4) V√Ĺpońćetn√≠ technika. VŇ°echny tŇôi str√°nky v√Ĺpońćetn√≠ techniky, tj. hardware, software a orgware mus√≠ b√Ĺt v rovnov√°ze.
5) Informańćn√≠ z√°kladna. KaŇĺd√Ĺ model je tŇôeba zaplnit vstupn√≠mi √ļdaji, kter√© vych√°zej√≠ z konkr√©tn√≠ch hodnovńõrn√Ĺch √ļdajŇĮ, zdŇĮvodnńõn√Ĺch norem a normativŇĮ. √ödaje mus√≠ b√Ĺt ve formńõ vhodn√© pro kvantifikaci modelu. Je tŇôeba vytv√°Ňôet specifick√© informańćn√≠ syst√©my (banky dat).
1.4.5. V√Ĺznam syst√©mov√©ho modelov√°n√≠
Ekonomicko matematick√© modely poskytuj√≠ srozumiteln√Ĺ popis vŇ°ech relevantn√≠ch faktorŇĮ dan√© situace a umoŇĺŇąuj√≠ odhalit podstatn√© vztahy mezi prvky studovan√©ho syst√©mu. PouŇĺit√≠ matematick√©ho modelu m√° Ňôadu v√Ĺhod:
1) UmoŇĺŇąuje zjistit informace o chov√°n√≠ syst√©mu,
i kdyŇĺ uńćinit z√°vńõry pŇô√≠mo z origin√°lu je nemoŇĺn√© nebo obt√≠Ňĺn√©.
2) Urychluje proces rozhodování. Procesy, které
ve skuteńćn√©m syst√©mu prob√≠haj√≠ pozvolna a dlouhodobńõ, lze pomoc√≠
modelu sledovat bńõhem nńõkolika okamŇĺikŇĮ.
3) UsnadŇąuje a racionalizuje rozhodovac√≠ proces.
Modelov√° forma zobrazen√≠ syst√©mu je pŇôehledn√°, struńćn√° a umoŇĺŇąuje
postup pŇôi ŇôeŇ°en√≠ probl√©mu podle potŇôeby uŇĺivatele. Modely vn√°Ň°ej√≠
poŇô√°dek do naŇ°eho myŇ°len√≠.
4) UmoŇĺŇąuje variantn√≠ ŇôeŇ°en√≠, tj. propońćet
cel√© Ňôady variant moŇĺn√Ĺch v√ĹsledkŇĮ.
5) OdstraŇąuje nebezpeńć√≠ vzniku ztr√°t v dŇĮsledku
chybného rozhodnutí (na rozdíl od experimentu v reálném systému).
Podrobnosti k probl√©mŇĮm syst√©mov√©ho modelov√°n√≠ lze nal√©zt ve skriptech: Z√≠skal, J.: Syst√©mov√° anal√Ĺza a modelov√°n√≠, 1. d√≠l, PEF, ńĆZU v Praze, Credit, Praha, 1998, str. 6-31, 32-49, 51-66.
1.4.6. Pozn√°mky o modelov√°n√≠ mńõkk√Ĺch syst√©mŇĮ
Syst√©mov√Ĺ pŇô√≠stup pŇôi ŇôeŇ°en√≠ ekonomick√Ĺch a spoleńćensk√Ĺch probl√©mŇĮ respektuje nejŇ°irŇ°√≠ souvislosti mezi jevy, a to se projevuje zcela nov√Ĺm, kvalitativn√≠m uvaŇĺov√°n√≠m a kvalitativn√≠ anal√Ĺzou syst√©mu, kdy se z√°jem manaŇĺera soustŇôeńŹuje i na oblasti zd√°nlivńõ s ŇôeŇ°en√Ĺm probl√©mem nesouvisej√≠c√≠: na souvislosti soci√°ln√≠, ekologick√©, sociologick√©, kulturn√≠, politick√©, estetick√©, mravn√≠, etick√©, na tradice a zvyklosti. Syst√©m, ve kter√©m se respektuj√≠ pŇôi rozhodov√°n√≠ tyto a podobn√© vlivy, se naz√Ĺv√° mńõkk√Ĺ syst√©m. Rozhodov√°n√≠ v mńõkk√Ĺch syst√©mech je rozhodov√°n√≠, a mus√≠ tedy splŇąovat i vŇ°echny z√°sady rozhodovac√≠ho procesu, tak jak byly pops√°ny v pŇôedchoz√≠ch odstavc√≠ch, zab√Ĺvaj√≠c√≠ch se probl√©my anal√Ĺzy "tvrd√Ĺch syst√©mŇĮ". Rozhodov√°n√≠ v mńõkk√Ĺch syst√©mech ovŇ°em vyŇĺaduje zvl√°Ň°tn√≠ postupy a speci√°ln√≠ podporu a je proto moŇĺno pro tyto postupy pouŇĺ√≠vat analogicky term√≠n mńõkk√© rozhodov√°n√≠.
Mńõkk√Ĺ syst√©m je semi-strukturovan√Ĺ, ale ne kaŇĺd√Ĺ semi-strukturovan√Ĺ syst√©m je mńõkk√Ĺ. Z hlediska teorie rozhodov√°n√≠ sice pŇôi ŇôeŇ°en√≠ probl√©mu prob√≠haj√≠ vŇ°echny f√°ze rozhodovac√≠ho procesu, ale techniky pouŇĺ√≠van√© pŇôi identifikaci probl√©mu, ŇôeŇ°en√≠, v√Ĺbńõru ŇôeŇ°en√≠ a implementaci jsou obecnńõ jin√© a obecnńõ sloŇĺitńõjŇ°√≠. Metody OR/MS, statistick√© a jin√© kvantitativn√≠ metody se tak√© v mńõkk√Ĺch syst√©mech uŇĺ√≠vaj√≠, ale podstatnńõ se mńõn√≠ metodologie jejich pouŇĺit√≠. Mńõkk√Ĺ syst√©m vymezujeme od tvrd√©ho syst√©mu v√Ĺńćtem vlastnost√≠ a zpravidla se odliŇ°n√© vlastnosti stav√≠ vedle sebe. Jako uk√°zku lze uv√©st napŇô. popis z√°kladn√≠ch zmńõn v pŇô√≠stupech k ŇôeŇ°en√≠ probl√©mŇĮ v prŇĮbńõhu historie, kter√Ĺ z√°roveŇą vymezuje i nńõkter√© podstatn√© vlastnosti mńõkk√©ho syst√©mu, tabulka 1.4.
Smńõr v√Ĺvoje
1960
1995
-----------------------------------------------------------------------------------------------------------------
ŇėeŇ°en√≠, metodologie
tvrdé
mńõkk√© algoritmick√©
heuristické
deterministické
neurńćit√©
Postupy, v√Ĺsledky
preference tvrd√Ĺch metodologi√≠
objevov√°n√≠ mńõkk√Ĺch
zkreslen√≠ skuteńćnosti
snahy o skuteńćnost
absolutn√≠ ŇôeŇ°en√≠
ŇôeŇ°en√≠ se skuteńćnosti pŇôibliŇĺuje
podŇô√≠zenost probl√©mu apar√°tu
nadŇôazenost probl√©mu
dobr√° strukturovatelnost
obt√≠Ňĺn√°, nemoŇĺn√°
tradińćn√≠ postupy, pŇô√≠stupy
kvalitativn√≠ uvaŇĺov√°n√≠
Tabulka 1.4 ‚ÄĚPorovn√°n√≠ nńõkter√Ĺch vlastnost√≠ tvrd√©ho a mńõkk√©ho syst√©mu‚ÄĚ
PŇôi postupech tvrdou metodologi√≠ se probl√©m matematicky formalizuje co nejpŇôesnńõji, sloŇĺit√Ĺ probl√©m se strukturuje podle potŇôeby algoritmŇĮ, ne podle sv√© povahy, je tedy ŇôeŇ°en√≠ takov√©ho probl√©mu podŇô√≠zeno apar√°tu, kter√Ĺ je v dan√© dobńõ k disposici. Tento postup je po form√°ln√≠ str√°nce bez probl√©mŇĮ, postup lze automatizovat a v podstatńõ pŇôen√°Ň°et na jin√© analogick√© situace. Ve v√Ĺchovńõ odborn√≠kŇĮ pŇôevl√°daj√≠ tzv. pŇô√≠padov√© studie (Case Study), na nichŇĺ si budouc√≠ specialist√© bystŇô√≠ vtip a uńć√≠ se standardizovan√© postupy, jeŇĺ by mńõli bez probl√©mŇĮ analogicky vyuŇĺ√≠vat ve sv√© praxi. Analogie ŇôeŇ°en√≠ probl√©mu je zde nosn√Ĺm prvkem uvaŇĺov√°n√≠. Jakmile je syst√©m modelov√°n, napŇô. soustavou rovnic, pozornost ŇôeŇ°itelŇĮ se jiŇĺ soustŇôeńŹuje na model a ztr√°c√≠ se z√°jem o realitu. Ne√ļspńõch metody se zdŇĮvodŇąuje Ň°patnńõ provedou implementańćn√≠ f√°z√≠.
Mńõkk√° metodologie vyŇĺaduje zcela jin√Ĺ pŇô√≠stup ve vŇ°ech f√°z√≠ch rozhodovac√≠ho procesu, tj. ve f√°zi identifikace, projektu, v√Ĺbńõru i implementace. ZdŇĮrazŇąuje se pŇôedevŇ°√≠m potŇôeba co nej√ļplnńõjŇ°√≠ho pozn√°n√≠ syst√©mu a jeho okol√≠ a co nejv√ĹstiŇĺnńõjŇ°√≠ popis probl√©mŇĮ bez ohledu na moŇĺnosti kvantifikace nebo form√°ln√≠ho popisu jevŇĮ. Nńõkdy nelze syst√©m formalizovat ryz√≠mi matematick√Ĺmi prostŇôedky, a pouŇĺ√≠vaj√≠ se proto rŇĮzn√© jin√© formy popisu. Syst√©m a probl√©m je napŇô. moŇĺno popsat nńõkolika pŇô√≠padov√Ĺmi studiemi, kter√© nemus√≠ zcela vystihovat vŇ°echny probl√©my, ale ŇôeŇ°√≠ problematiku z nńõkolika hledisek. VyuŇĺ√≠v√° se skupin expertŇĮ, panelov√Ĺch diskus√≠, neform√°ln√≠ch z√°pisŇĮ. PŇôi ŇôeŇ°en√≠ probl√©mu v mńõkk√©m syst√©mu neb√Ĺv√° v√Ĺsledkem jednoznańćn√© a koneńćn√© ŇôeŇ°en√≠. ŇėeŇ°en√≠ se mŇĮŇĺe jevit jako doporuńćen√≠ a nemus√≠ b√Ĺt jednoznańćn√©. I v√Ĺsledek, kter√Ĺ pom√°h√° pochopit tendence zmńõn v mńõkk√©m syst√©mu, mŇĮŇĺe b√Ĺt akceptov√°n jako √ļspńõŇ°n√Ĺ. PŇôi ŇôeŇ°en√≠ praktick√Ĺch aplikac√≠ nen√≠ vhodn√© pŇô√≠snńõ rozliŇ°ovat mezi tvrd√Ĺmi a mńõkk√Ĺmi syst√©my - jeden a t√ĹŇĺ syst√©m se mŇĮŇĺe z urńćit√©ho pohledu jevit jako tvrd√Ĺ, z jin√©ho pohledu vyŇĺaduje pouŇĺit√≠ mńõkk√© technologie. ŇėeŇ°itel tedy mus√≠ oba postupy vyuŇĺ√≠vat a vz√°jemnńõ doplŇąovat. Pro ŇôeŇ°en√≠ mńõkk√Ĺch syst√©mŇĮ je podle Checklanda (1976) tŇôeba nahradit interdisciplin√°rn√≠ koncepci transdisciplin√°rn√≠ (transdisciplinary concepts). Transdisciplin√°rn√≠ koncepce ŇôeŇ°en√≠ probl√©mŇĮ pŇôedpokl√°d√° pŇôekon√°n√≠ hranic i mezi znańćnńõ vzd√°len√Ĺmi vńõdn√≠mi obory a sjednocen√≠ jejich poznatkŇĮ.
Metodologie tvrd√Ĺch syst√©mŇĮ byla vypracov√°na v r√°mci syst√©mov√©ho inŇĺen√Ĺrstv√≠, syst√©mov√© vńõdy i obecn√© teorie syst√©mŇĮ a pŇôi ŇôeŇ°en√≠ probl√©mŇĮ v tvrd√Ĺch syst√©mech v podstatńõ vyhovuje. Je to rozs√°hl√Ĺ a mnohokr√°te ovńõŇôen√Ĺ apar√°t zaloŇĺen√Ĺ na teorii modelov√°n√≠, teorii rozhodov√°n√≠, OR/MS a dalŇ°√≠ch kvantitativn√≠ch discipl√≠n√°ch. PŇôednost√≠ tvrd√© metodologie je snadn√° algoritmizovatelnost postupŇĮ, pŇôenositelnost z jednoho analogick√©ho probl√©mu na druh√Ĺ, moŇĺnost automatizace postupŇĮ a i jist√° elegance a pŇôesnost v popisu modelŇĮ a postupŇĮ pŇôi jejich anal√Ĺze.
Metodologie mńõkk√Ĺch syst√©mŇĮ je ve sv√©m pojet√≠ Ň°irŇ°√≠ a metodologii tvrd√Ĺch syst√©mŇĮ obsahuje jako svoji souńć√°st. Rozmach mńõkk√Ĺch metodologi√≠ je v posledn√≠ch l√©tech znańćn√Ĺ. Mńõkk√° metodologie je zaloŇĺena na tzv. metapŇô√≠stupech syst√©mov√© vńõdy a snaŇĺ√≠ se o dokonal√© vystiŇĺen√≠ vlastnost√≠ syst√©mu, nńõkdy i na √ļkor form√°ln√≠ elegance zobrazen√≠. Metodicky je to pŇô√≠stup nehomogenn√≠, obecnńõ nepŇôenosn√Ĺ, nedovoluje exaktn√≠ zjiŇ°tńõn√≠, zda bylo dosaŇĺeno optim√°ln√≠ho exaktn√≠ho ŇôeŇ°en√≠, uŇĺivatel se mus√≠ ve vńõtŇ°inńõ pŇô√≠padŇĮ spokojit s dosti dobr√Ĺm ŇôeŇ°en√≠m. Mńõkk√° metodologie je humanistick√° v tom smyslu, Ňĺe zahrnuje vliv lidsk√©ho ńćinitele uvnitŇô i v okol√≠ syst√©mu v nejŇ°irŇ°√≠ch aspektech psychick√Ĺch, soci√°ln√≠ch, sociologick√Ĺch a politick√Ĺch.
Havl√≠ńćek J., Z√≠skal J.: Mńõkk√© metodologie v syst√©mech pro podporu rozhodov√°n√≠. Zemńõdńõlsk√° ekonomika, 42, 1996 (9), str. 425-433.
Jako ilustrace mńõkk√Ĺch metodologi√≠ lze
uv√©st tzv. JenkinsŇĮv akńćn√≠ v√Ĺzkum a Checklandovu metodologie mńõkk√Ĺch
syst√©mŇĮ.
Akńćn√≠ v√Ĺzkum podle Jenkinse obsahuje ńćtyŇôi
f√°ze, pŇôipom√≠naj√≠c√≠ Simonovo ńćlenńõn√≠. Jsou to (i) identifikace,
(ii) projekt, (iii) implementace, (iv) sledov√°n√≠ provozu a pŇô√≠padnńõ
nov√Ĺ projekt a nov√° implementace. V kaŇĺd√© f√°zi se respektuj√≠ strategick√°
pravidla: (1) identifikace se prov√°d√≠ kombinac√≠ tvrd√Ĺch i mńõkk√Ĺch
postupŇĮ, vyuŇĺ√≠v√° se expertŇĮ, (2) probl√©m konfliktn√≠ch situac√≠ se
ŇôeŇ°√≠ metodami vah nebo jako v√≠cekriteri√°ln√≠ probl√©m, (3) probl√©m
se strukturuje, postupuje se v iterac√≠ch, (4) koneńćn√Ĺ v√Ĺstup se ovńõŇôuje
v praxi pomoc√≠ experiment√°ln√≠ho ovńõŇôen√≠, nebo pomoc√≠ expertŇĮ.
Checkland vych√°zel ve sv√© metodologii z Jenkinsov√Ĺch zkuŇ°enost√≠. Na rozd√≠l od Jenkinse pŇôedpokl√°d√°, Ňĺe jeden a t√ĹŇĺ probl√©m mŇĮŇĺe b√Ĺt ŇôeŇ°en a hodnocen z rŇĮzn√Ĺch pohledŇĮ rŇĮznńõ a pŇôi ŇôeŇ°en√≠ je tedy tŇôeba souńćasnńõ postupovat nejm√©nńõ ve dvou √ļrovn√≠ch. Tyto dvńõ √ļrovnńõ jsou (i) vhodn√Ĺ model reality s aktivn√≠m zapojen√≠m a angaŇĺovanost√≠ lid√≠ (tj. nemus√≠ se jednat o form√°ln√≠ matematick√Ĺ model), (ii) abstraktn√≠ model vyŇ°Ň°√≠ √ļrovnńõ. Po obou √ļrovn√≠ch se postupuje soubńõŇĺnńõ ve vz√°jemn√© interakci. Postup je rozpracov√°n do 7 f√°z√≠ : (1) popis probl√©mov√© situace, (2) strukturov√°n√≠ a identifikace probl√©mu, (3) vymezen√≠ subsyst√©mŇĮ, jejichŇĺ anal√Ĺza povede k ŇôeŇ°en√≠ probl√©mu - realizace CATWOE, (4) tvorba projektu, modelu, (5) tvorba koncepce, konceptu√°ln√≠ho modelu, (6) v√Ĺbńõr ŇôeŇ°en√≠ a implementace, (7) sledov√°n√≠ zpńõtn√© vazby a opravy ŇôeŇ°en√≠.
Metodologie tvrd√Ĺch syst√©mŇĮ vych√°z√≠ z matematick√Ĺch principŇĮ a matematick√Ĺch pŇô√≠stupŇĮ k anal√Ĺze syst√©mu. V pŇô√≠padńõ mńõkk√Ĺch syst√©mŇĮ se naopak hledaj√≠ prostŇôedky jak probl√©m dokonale popsat a syst√©m zobrazit, tŇôeba i nematematick√Ĺmi prostŇôedky a za v√°gn√≠ch pŇôedpokladŇĮ. Skupiny takov√Ĺch metod a postupŇĮ se naz√Ĺvaj√≠ metametodologie. Prvn√≠m a nejdŇĮleŇĺitńõjŇ°√≠m √ļkolem metametodologie je popis postupu, kter√Ĺ bychom mohli nazvat jako vytvoŇôen√≠ metodologie metodologi√≠. Od takov√©ho postupu se potom odvozuj√≠ dalŇ°√≠ metakonstrukce v syst√©mov√© vńõdńõ jako jsou metametodologick√© dotazov√°n√≠, modelov√°n√≠, apod. Nńõkter√© postupy metametodologie lze popsat matematicky, nńõkter√© je nutno vyj√°dŇôit empiricky. Mezi empirick√© metody patŇô√≠ napŇô. expertn√≠ anal√Ĺza, vyj√°dŇôen√≠ skuteńćnosti pomoc√≠ subjektivn√≠ pravdńõpodobnosti, pouŇĺit√≠ fuzzy jazykov√Ĺch oper√°torŇĮ, simulace.
V souvislosti s rozvojem metametodologi√≠ (metamodelov√°n√≠, metasyst√©mŇĮ) je vhodn√© uv√©st zaj√≠mavou klasifikaci vńõd a vńõdeck√Ĺch pŇô√≠stupŇĮ k ŇôeŇ°en√≠ probl√©mŇĮ, kterou uv√°d√≠ Rosen (1986) a kter√° vymezuje postaven√≠ mńõkk√©ho syst√©mu v souńćasn√© vńõdńõ. Souńćasnou vńõdu a jej√≠ pŇô√≠stupy charakterizuje jako dvourozmńõrnou vńõdu (Two-Dimensional Science), coŇĺ je vńõda v informańćn√≠m prostŇôed√≠. PrŇĮmyslov√° spoleńćnost produkuje jednorozmńõrnou vńõdu (One-Dimensional Science), kter√° je charakteristick√° experimentov√°n√≠m. Rozvoj umńõl√© inteligence pŇôid√° v pŇô√≠Ň°t√≠m stolet√≠ vńõdńõ zŇôejmńõ dalŇ°√≠ dimenzi.
1.5. Shrnutí
Kvantitativn√≠ metody a pŇô√≠stupy vyuŇĺ√≠v√° management pro podporu rozhodov√°n√≠. Jsou soustŇôedńõny ve vńõdn√≠ discipl√≠nńõ Management Science/Operation Research (MS/OR). Rozhodovac√≠ proces prob√≠h√° v etap√°ch a je pro nńõj charakteristick√© vyuŇĺ√≠v√°n√≠:
1.6. Kl√≠ńćov√° slova
DobŇôe strukturovan√Ĺ probl√©m, nestrukturovan√Ĺ probl√©m, semistrukturovan√Ĺ probl√©m, f√°ze rozhodovac√≠ho procesu (Intelligence, Design, Choice), rozhodov√°n√≠ za jistoty, rozhodov√°n√≠ za rizika, vńõdeck√Ĺ pŇô√≠stup k rozhodov√°n√≠, syst√©mov√© modelov√°n√≠, matematick√Ĺ model, zaveden√≠ syst√©mu, kvantifikace, interpretace, implementace, Management Science, Operańćn√≠ v√Ĺzkum, Operańćn√≠ anal√Ĺza, t√Ĺmov√° pr√°ce, syst√©mov√Ĺ pŇô√≠stup, matematick√© programov√°n√≠, s√≠Ň•ov√° anal√Ĺza, strukturn√≠ anal√Ĺza, simulańćn√≠ metody, teorie her, syst√©mov√Ĺ model, mńõkk√Ĺ syst√©m, mńõkk√° metodologie, metapŇô√≠stupy.
1.7. Ot√°zky ke studiu
1. Jak√° je podstata manaŇĺersk√©ho rozhodov√°n√≠?
2. Vysvńõtlete jednotliv√© f√°ze rozhodovac√≠ho
procesu.
3. Specifikujte odliŇ°nosti dobŇôe strukturovan√Ĺch
a nestrukturovan√Ĺch probl√©mŇĮ.
4. Jak√° je podstata vńõdeck√©ho pŇô√≠stupu k rozhodov√°n√≠?
5. PopiŇ°te postup pŇôi matematick√©m modelov√°n√≠.
6. Charakterizujte Management Science.
7. UveńŹte n√°zvy disciplin, kter√© lze zaŇôadit
mezi kvantitativní metody.
8. UveńŹte pŇôedpoklady √ļspńõŇ°n√©ho vyuŇĺ√≠v√°n√≠
kvantitativních metod.
9. Jak√© jsou v√Ĺhody t√Ĺmov√©ho ŇôeŇ°en√≠ probl√©mŇĮ?
10. Vysvńõtlete podstatu syst√©mov√©ho pŇô√≠stupu.
11. Z√°kladn√≠ charakteristiky mńõkk√©ho syst√©mu.
1.8. Studijní literatura
1. Klir J.G.: Facets of Systems Science, Plenum Press, N.Y. 1991, 664 str.
1. MS - aplikace, metodologie aplikací,
syst√©mov√° podpora rozhodov√°n√≠ atd. OR - teorie, tvorba algoritmŇĮ,
teoretick√Ĺ rozvoj vńõdn√≠ discipl√≠ny
2. Ne. Simon povaŇĺuje implementaci
za samostatn√Ĺ probl√©m, kter√Ĺ je tŇôeba posuzovat samostatnńõ z hlediska
jeho tŇô√≠ f√°z√≠: Intelligence, Design, Choice. Existuj√≠ ale jin√© klasifikace
postupŇĮ pŇôi ŇôeŇ°en√≠ probl√©mu: napŇô. Sol, H.G.: Simulation in Information
Systems Development, University of Groningen, 1982, rozliŇ°uje aŇĺ
10 f√°z√≠, vńćetnńõ implementace. Podobnńõ napŇô. i Bosman, Einhorn a Gogart
navrhuj√≠ v√≠ce f√°z√≠. Simonova klasifikace je ale povaŇĺov√°na za nejlepŇ°√≠.
5. Ve vŇ°ech pŇô√≠padech lze naj√≠t
probl√©my jejichŇĺ ŇôeŇ°en√≠ je standardn√≠ a pŇôedstavuj√≠ proto dobŇôe
strukturovan√© situace (standardn√≠ v√Ĺrobn√≠ a provozn√≠ postupy, technologie).
VńõtŇ°ina ostatn√≠ch probl√©mŇĮ jsou probl√©my semistrukturovan√©.
6. ŇĹ√°dn√Ĺ.
9. Uvńõdomte si, Ňĺe v mnoha probl√©mech
je tŇôeba respektovat i ekologick√© aspekty, soci√°ln√≠ aspekty. Ekologick√Ĺ
aspekt vyŇĺaduje splnńõn√≠ dalŇ°√≠ch c√≠lŇĮ - napŇô. recyklaci obalŇĮ,
minimalizaci z√°boru pŇĮdn√≠ho fondu, minim√°ln√≠ spotŇôebu nńõkter√Ĺch
zdrojŇĮ atd.
10. V absolutn√≠m pojet√≠ Ňĺ√°dn√°
ńćinnost neprob√≠h√° za jistoty. V praktick√©m Ňĺivotńõ ale u nńõkter√Ĺch
ńćinnost√≠ mŇĮŇĺeme na z√°kladńõ dlouhodob√Ĺch zkuŇ°enost√≠ jistotu pŇôedpokl√°dat:
j√≠t na pivo, vytrŇĺen√≠ zubu pokud hodnńõ bol√≠, nebo zkouŇ°ka z EMM pokud
jsem dobŇôe pŇôipraven, ukl√°dat √ļspor pr√°vńõ u ńćtyŇô √ļstavŇĮ do v√ĹŇ°e
400 000 Kńć pŇôi garanci st√°tu, atd. PŇôi volbńõ povol√°n√≠ nadan√©ho
d√≠tńõte mohu stanovit pravdńõpodobnost zamńõstn√°n√≠ v urńćit√© profesi.
Podobnńõ lze zjistit, s jakou pravdńõpodobnost√≠ um√≠raj√≠ lid√©, kteŇô√≠
nepij√≠ ml√©ko. Za nejistoty se rozhoduji napŇô. pŇôi kup√≥nov√© privatizaci.
11. VŇĺdy se jedn√° o pomńõr mezi
vstupy a v√Ĺstupy. NapŇô. u dom√°cnosti lze √ļńćinnost funkce manŇĺelky
vyj√°dŇôit jako pomńõr mezi jej√≠mi n√°klady na chod dom√°cnosti a cenou,
kterou by bylo nutno zaplatit sjednan√© hospodyni. Efektivnost n√°vŇ°tńõvy
kurzu Ň°it√≠, kter√Ĺ manŇĺelka (dobrovolnńõ) absolvuje, lze mńõŇôit pomńõrem
n√°kladŇĮ spotŇôebovan√Ĺch po absolvov√°n√≠ kurzu s n√°klady pŇôed kurzem.
12. UvaŇĺujte n√°klady spojen√© s
proŇ°kolov√°n√≠m mimo dosaŇĺen√≠ vzdńõl√°n√≠, zakoupen√≠m pŇô√≠ruńćek,
pomŇĮcek, sluŇĺeb.