1

2. Základní pojmy lineárního programování

Učební cíle

Po prostudování této kapitoly byste měli:

Porozumět principům optimalizace při daných omezeních.
Dokázat formulovat model lineárního programování (LP).
Umět graficky řešit úlohu LP se dvěma proměnnými.
Pochopit obecné vlastnosti přípustných řešení úlohy LP.

V této kapitole se budeme zabývat skupinou manažerských problémů, které se řeší pomocí metod matematického programování. Tyto problémy lze obecně charakterizovat takto:

Je možno realizovat větší počet činností (procesů) v různých kombinacích a je třeba stanovit podle určitého hlediska (např. maximalizace zisku) optimální kombinaci těchto činností za předpokladu, že jejich realizace je omezena disponibilním množstvím výrobních kapacit (zdrojů) a různými požadavky, které jsou na činnosti kladeny (např. požadavky odbytu na sortiment aj.). Problémy, ve kterých je cílem co nejlépe umístit (alokovat) omezené zdroje a nalézt optimální vazby mezi zdroji a potřebami se nazývají alokační problémy.

Jednou z nejrozšířenějších a nejpropracovanějších metod pro řešení alokačních problémů je lineární programování. Proto se v této kapitole zaměříme na vysvětlení podstaty a principů řešení úloh lineárního programování. Správné pochopení této kapitoly vyžaduje nezbytné matematické znalosti konvexních množin, lineárních nerovností a vektorového počtu.

Požadovaný matematický náhled: Slavík, V. a kol.: Matematika II, skripta, ČZU v Praze, Technická fakulta, Praha 1998.

2.1 Formulace modelu lineárního programování

2.1.1 Úvodní poznámka

Obecný model lineárního programování (LP) byl vytvořen při řízení výroby a organizaci hospodářství v průběhu II. světové války ve Velké Britanii a USA.

V létech 1940-45 vypracoval G. B. Dantzig simplexovou metodu, univerzální algoritmus pro řešení úloh LP. T. C. Koopmans publikoval “distribuční model”, který je v podstatě specifickým případem Dantzigova obecného modelu. V roce 1951 A. Charnes a W. W. Cooper začali využívat LP ve výrobě. V následujících létech R. Bellman vytvořil teoretické a matematické základy pro dynamické programování. Největší rozvoj LP nastal pak v létech 1955-60.

2.1.2 Význam lineárního programování

1. Rozvoj zájmu o kvantitativní modely hospodářských soustav, vědecké řízení a plánování výroby.
2. Nový systémový pohled na činnosti výrobců a průmyslníků.
3. Rozvoj výzkumné činnosti v analýze hospodářských soustav.
4. Vědecký nástroj řízení.

Problémů, které lze řešit pomocí LP je mnoho a jsou velmi rozmanité. Uvedeme ve zjednodušené podobě dva typické problémy lineárního programování.

2.1.3 Příklad

Podnik vyrábí dva výrobky V₁ a V₂, které se zpracovávají na dvou typech strojů A a B. Zhotovení jednotky výrobku V₁ vyžaduje 6 strojových hodin na stroji typu A a 3 hodiny práce na stroji typu B. Obdobně zhotovení výrobku V₂ vyžaduje 4 strojové hodiny jak na stroji A tak i na stroji B. Podnik má měsíčně k dispozici celkem 3 000 strojových hodin na strojích typu A a 2500 strojových hodin na strojích typu B. Cena jednotky výrobku V₁ činí 200 Kč a cena výrobku V₂ je 300 Kč. Podnik má zaručený odbyt obou výrobků a není vázán na určitý sortiment. Je třeba rozhodnout, kolik má podnik vyrobit jednotlivých výrobků, aby dosáhl co nejvyšší celkové ceny odbytu.

2.1.4 Příklad

Management zemědělského podniku musí vyřešit následující problém:

Na ploše 14 ha, která nemusí být plně využitá, je třeba pěstovat plodiny A a B tak, aby se dosáhlo maximální produkce. Je požadováno vyrobit alespoň 32 tun krmných jednotek a plodinu A lze vzhledem k osevnímu postupu pěstovat nejvýše na 11 ha. K dispozici je celkem 100 hodin lidské práce a ostatní výrobní faktory nejsou limitovány. Nároky a výnosy jednotlivých plodin na výrobní faktory jsou uvedeny v následující tabulce.

Na 1 ha	Plodina A B
Výnos krmných jednotek (t)	4	2
Potřeba hodin lidské práce	5	10
Plánovaná produkce (tis. Kč)	3	2

2.1.5 Příklad formulace modelu lineárního programování

Uvedený příklad 2.1.4. požaduje určení optimální výrobní struktury uvažovaných plodin A a B tak, aby bylo dosaženo maximální produkce. Pomocí daných výrobních zdrojů (půda a lidská práce) může zemědělský podnik pěstovat dvě různé plodiny, které přinášejí různou výši produkce z jednoho hektaru. Vztah mezi činiteli výroby a výsledky je dán v podkladové tabulce.
Označme:

x₁ … hledanou plochu plodiny A
x₂ … hledanou plochu plodiny B

Pak bude celková disponibilní plocha v případě, že nepožadujeme plně její využití, formulována nerovnicí:

x₁ + x₂ £ 14.

Pro omezené množství hodin lidské práce musí platit:

5x₁ + 10x₂ £ 100.

Protože se požaduje produkce alespoň 32 tun krmných jednotek, lze formulovat požadované omezení:

4x₁ + 2x₂ ³ 32.

Omezení plochy plodiny A nejvýše na 11 ha představuje kapacitní omezení:

x₁ £ 11.

Každý výrobní program lze nyní vyjádřit ve formě dvojice reálných čísel x₁a x₂, které vyhovují všem uvedeným nerovnostem. Proměnné x₁a x₂, které vyjadřují hledanou výměru plodin A a B nazýváme rozhodovací (decision variable) proměnné. Reálným výrobním programem bude jen nezáporná dvojice reálných čísel x₁, x₂, a proto je třeba ještě formulovat podmínku nezápornosti řešení:

x₁ ³ 0, x₂ ³ 0.

Nezáporná řešení x₁, x₂ všech uvedených nerovnic představují pro zemědělský podnik reálné výměry uvažovaných plodin. Takových reálných výměr (přípustných řešení) existuje nekonečně mnoho. Cílem je ale nalezení takové struktury výměry obou plodin, při které se dosahuje maximální produkce. Vyjádříme proto cíl optimalizace číselně v podobě účelové (kriteriální) funkce:

z = 3x₁ + 2x₂ ®max.

Koeficienty ve funkci z se nazývají ceny (sazby). Matematický model našeho problému je tedy formulován takto: je třeba nalézt maximum účelové

funkce.z_max = 3x₁ + 2x₂(2.1)

za podmínek

x₁ + x₂ £ 14 (2.2)
5x₁ + 10x₂ £ 100 (2.3)
4x₁ + 2x₂ ³ 32 (2.4)
x₁£ 11 (2.5)
x₁³ 0, x₂ ³ 0 (2.6)

Kontrolní otázky:

1. Definujte rozhodovací proměnné v příkladě 2.1.3.

2. Napište matematický model LP pro příklad 2.1.3. Postupujte obdobně jako v příkladě 2.1.4.

2.1.6 Postup při formulaci modelu lineárního programování

Verbální model

Vymezení a identifikace problému
Verbální popis problému (popis jednotlivých izolovaných procesů)
Stanovení cíle

Kvantifikace jednotlivých prvků (podkladová tabulka)

Ekonomicko-matematický model LP

Definování proměnných, jejichž hodnoty máme nalézt. Vymezení jejich nezápornosti.
Formulace omezujících podmínek zobrazujících vztahy mezi procesy pomocí soustavy lineárních nerovnic, resp. rovnic
Formulace kriteriální lineární funkce, vyjadřující cíl výpočtu (kriteriální funkce slouží k posouzení výhodnosti jednotlivých procesů).

2.1.7 Obecná formulace modelu lineárního programování

Model lineárního programování (2.1) až (2.6) lze obecně vyjádřit matematickým zápisem takto:

máme najít extrém účelové funkce

za podmínek:

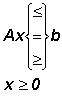Matice je matice typu (m, n) a nazývá se matice soustavy omezujících podmínek, je vektor proměnných, je vektor pravých stran soustavy omezujících podmínek, je vektor cen.

S matematickým modelem LP a jeho vlastnostmi se podrobně seznámíte ve 3. kapitole.

Kontrolní otázky:

3. Uvažujte model LP (2.1) - (2.6).

Pokuste se najít odhadem alespoň dvě různá přípustná řešení!
Spočtěte hodnotu účelové funkce u těchto řešení!

4. Určete libovolné nepřípustné řešení!
5. Dokážete najít v modelu (2.1) - (2.6) omezující podmínku, kterou by bylo možno přetvořit na minimalizační účelovou funkci?

2.2 Grafické řešení úlohy lineárního programování

2.2.1 Úvodní poznámka

Geometrická interpretace lineárních nerovnic a vlastnosti konvexních množin umožňují řešit úlohu LP graficky. Grafická metoda se používá pro řešení úloh LP se dvěma proměnnými a konečným počtem omezujících podmínek. Metoda je prakticky málo využitelná, neboť v praxi se zřídka vyskytují jednoduché problémy pouze se dvěma proměnnými. Význam grafické metody spočívá v názorné interpretaci základních vlastností modelu LP.

2.2.2 Postup při grafickém řešení modelu lineárního programování

1. Formulace matematického modelu.

2. Grafické vymezení množiny přípustných řešení.

3. Grafické zobrazení průběhu účelové funkce.

4. Nalezení extrému (maxima, minima) účelové funkce.

Postup při grafickém řešení budeme ilustrovat na řešení příkladu 2.1.4.
1. Matematický model úlohy je vyjádřen účelovou funkcí (2.1) a soustavou nerovnic (2.2) -(2.6):

z_max = 3x₁ + 2x₂(2.1)

x₁ + x₂ £ 14 (2.2)

5x₁ + 10x₂ £ 100 (2.3)

4x₁ + 2x₂ ³ 32 (2.4)

x₁£ 11 (2.5)

x₁ ³ 0, x₂ ³ 0 (2.6)

2. Geometrickým obrazem lineární nerovnice (2.2)

x₁ + x₂ £ 14

je polorovina o hraniční přímce x₁+ x₂ = 14.Zobrazíme nejprve hraniční přímku hledané poloroviny. Zaměření poloroviny určíme buď pomocí normálového vektoru hraniční přímky, nebo dosazením souřadnic vhodného bodu do nerovnice.

Na obrázku 2.1 je hraniční přímka poloroviny (2.2) označena číslem (2). Zaměření poloroviny jsme stanovili dosazením souřadnic počátku soustavy souřadnic [0,0] do nerovnice (2.2); souřadnice počátku dané nerovnici vyhovují, hledaná polorovina tedy obsahuje počátek souřadnic.

Podobným způsobem byly zobrazeny zbývající nerovnice (2.3) - (2.5). Na obrázku 2.1 jsou označeny postupně čísly (3) - (5). Podmínky nezápornosti (2.6) vymezují I. kvadrant.

Průnikem všech polorovin je konvexní polyedr (mnohoúhelník), jehož vnitřní a hraniční body [x₁, x₂] vyhovují zároveň všem nerovnicím úlohy. Konvexní polyedr představuje množinu všech přípustných řešení úlohy. Jeho vrcholy jsou na obrázku 2.1 označeny P₁, ..., P₅.

Figure 2.1 "Grafické řešení úlohy lineárního programování

3. Účelová funkce (2.1) je tzv. lineární funkcionál, který graficky představuje soustavu rovnoběžných přímek o parametru z. Dosadíme za z vhodné číslo, např. hodnotu z = 50 a zobrazíme přímku 3x₁ + 2x₂ = 50. Na obrázku 2.1 je zobrazena tečkovaně. Protože tato přímka neprotíná konvexní polyedr, není dosažení 50 tis. Kč produkce za daných omezujících podmínek reálné.

4. Při větší hodnotě z se přímka účelové funkce od polyedru vzdaluje, při menší hodnotě z se k polyedru přibližuje. Přímku účelové funkce musíme posunout rovnoběžně tak, aby měla s konvexním polyedrem aspoň jeden společný bod, což je v našem případě bod P₃. Optimálnímu řešení maximalizační úlohy odpovídá ten vrchol konvexního polyedru (vrchol P₃), kterým prochází přímka účelové funkce a přitom zůstává co nejdále od počátku (při minimalizaci je tomu naopak). Souřadnice bodu P₃ jsou hledané hodnoty proměnných x₁ a x₂. Určíme je buď přímo z obrázku, nebo výpočtem jako souřadnice průsečíku přímek (2) a (5). Zjistíme hodnoty x₁ = 11, x₂ = 3.

5. Dosazením těchto hodnot do rovnice účelové funkce zjistíme, že při pěstování plodiny A na ploše 11 ha a plodiny B na ploše 3 ha lze dosáhnout maximální produkce 39 tis. Kč. Míru využití ostatních zdrojů a splnění požadavků určíme postupným dosazením řešení x₁ = 11 a x₂ = 3 do jednotlivých nerovnic soustavy omezujících podmínek (2.2) - (2.6). Disponibilní plocha 14 ha bude plně využita, ze 100 hodin lidské práce zůstane 15 nevyužito a požadavek na výrobu 32 tun krmných jednotek bude překročen o 18 tun.

Kontrolní otázky:

Jak by se změnilo optimální řešení, kdyby:
6. došlo ke zvýšení produkce plodiny B na 3 tis. Kč?
7. plocha plodiny A nebyla omezena na 11 ha?

2.2.3 Postup při grafickém řešení modelu lineárního programování v QSB

Grafickou metodu řešení úloh LP obsahuje programový systém QSB

SW produkt QSB umožňuje řešit modely LP, které mají 2 rozhodovací proměnné a nejvýše 10 omezujících podmínek.
Po nastartování systému QSB (qsb.exe) se objeví hlavní nabídka možností programu. Standardní help (F1) popisuje jednotlivé kroky.

Poznámky k použití programu pro grafické řešení modelu LP:

1. volte nabídku “Linear Programming”

2. v dalším menu volte nabídku “Enter new Programm”

3. poznámky k volbě parametrů:

number of variables: udává se počet rozhodovacích proměnných
number of constraints: udává se počet omezujících podmínek bez podmínek nezápornosti
deafault variables names: zadejte číslo “1”
ostatní nabídky ignorujte nebo zadejte “0”

4. v dalším postupu sledujte pokyny v posledním řádku (“space bar” = mezerník)
5. volte krok “Solve Problem” potom nabídku “Graphic Method”

při nabídce určení měřítka na osách X a Y volte pro obě osy číslo “1”

6. Další doporučení pro užívání programu:

zadejte si nejprve příklad, který je spočten ve skriptech a porovnejte výsledky
zadávejte si jiné příklady, které najdete ve skriptech, nebo které si sami sestavíte
při zadávání dat se používají klávesy “Enter”, “Back space”, “/”, “Delete” - funkce dalších kláves jsou popsány v helpech (F1)
naučte se zadaný příklad upravit pomocí nabídky “Modify Problem”

2.3 Obecné vlastnosti přípustných řešení úlohy lineárního programování

2.3.1 Poznámka

Z grafického řešení úlohy LP lze odvodit některé základní vztahy mezi konvexní množinou řešení omezujících podmínek a vlastnostmi úlohy LP.

2.3.2 Definice

Množina bodů se nazývá konvexní, jestliže splňuje podmínku: patří-li do ní dva různé body, patří do ní také všechny body úsečky určené oběma body.

2.3.3 Poznámka k definici

Jsou-li dány dva body (vektory) A a B, potom lze body úsečky určené těmito body vyjádřit analyticky jako konvexní kombinaci obou bodů. Konvexní kombinace bodů A a B je definována jako bod C, pro který platí

C = kA + (1–k)B, 0

Definici 2.3.2 lze tedy alternativně formulovat také takto: Množina bodů se nazývá konvexní, jestliže splňuje podmínku: patří-li do ní dva různé body, patří do ní také jejich konvexní kombinace.

2.3.4 Příklad

Na obrázku 2.2 je množina a) nekonvexní b) konvexní.

Figure 2.2 ”Konvexní a nekonvexní množina”

2.3.5 Věta

Množina přípustných řešení úlohy LP je konvexní množina s konečným počtem vrcholů.

Důkaz:
Dokážeme, že množina přípustných řešení úlohy LP je konvexní. K tomu stačí podle poznámky 2.3.3. dokázat, že každá konvexní kombinace dvou přípustných řešení úlohy LP je opět přípustné řešení úlohy LP.

Nechť x₁ a x₂ jsou přípustná řešení úlohy LP. Nechť dále platí:

Ax₁ = b

Ax₂ = b

Konvexní kombinaci obou vektorů přípustných řešení lze psát ve tvaru podle definice 2.3.2.

x = kx₁ + (1 – k)x₂, kde 0 £ k £ 1.

Pro vektor x zřejmě platí:

Ax =A[kx₁ + (1– k)x₂]= kAx₁ + (1– k)Ax₂ = kb + (1– k)b = b.

Je tudíž x také přípustné řešení a množina přípustných řešení je konvexní. Platnost druhé části věty vyplývá z předpokladu, že model LP má konečný počet omezujících podmínek.

2.3.6 Klasifikace množin přípustných řešení v modelu lineárního programování

1. Množina přípustných řešení je prázdná. Omezující podmínky modelu LP jsou nekonzistentní a model nemá řešení, jak je uvedeno na obrázku 2.3.

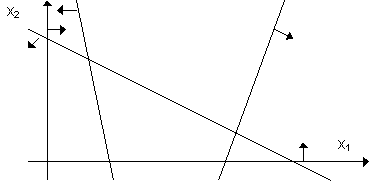
Figure 2.3 ”Prázdná množina řešení”

2. Množina přípustných řešení je konvexní polyedr. Model LP má nutně optimální řešení:

jediné řešení, když přímka účelové funkce se dotkne vrcholu polyedru
nekonečně mnoho řešení, když přímka účelové funkce protíná konvexní polyedr ve dvou vrcholech, obrázku 2.4.

Ve vícerozměrném prostoru je množina přípustných řešení modelu LP zobrazena jako konvexní vícerozměrný polyedr. V trojrozměrném prostoru je to konvexní mnohostěn, ve vícerozměrných prostorech konvexní nadmnohostěn. Účelová funkce je v trojrozměrném prostoru zobrazena rovinou, ve vícerozměrných prostorech nadrovinou. Ve vícerozměrném prostoru je množina přípustných řešení modelu LP zobrazena jako konvexní vícerozměrný polyedr. V trojrozměrném prostoru je to konvexní mnohostěn, ve vícerozměrných prostorech konvexní nadmnohostěn. Účelová funkce je v trojrozměrném prostoru zobrazena rovinou, ve vícerozměrných prostorech nadrovinou.

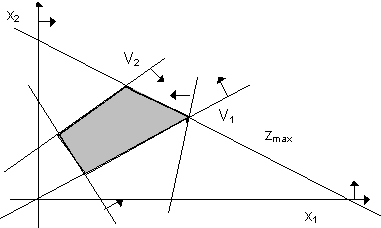
Figure 2.4 ”Konvexní polyedr”

Ve vícerozměrných prostorech se účelová funkce (nadrovina) může dotknout množiny přípustných řešení (nadmnohostěnu, polyedru) ve více vrcholech. V trojrozměrném prostoru ve třech vrcholech; potom se dotýká množiny přípustných řešení v celé stěně. Analogicky ve vícerozměrných prostorech se může dotknout ve více vrcholech.

3. Množina přípustných řešení je neohraničená. Účelová funkce může při maximalizaci na množině přípustných řešení nabývat libovolně velkých hodnot. Na obrázku 2.5 je hodnota účelové funkce na množině řešení shora neohraničená.

Figure 2.5 ”Neohraničená konvexní množina”

Kontrolní otázky:

8. Podívejte se na obrázek 2.4.; za předpokladu, že na osách x₁ax₂je měřítko 1 cm.

Odhadněte souřadnice vrcholů V₁a V₂!
Určete souřadnice středu úsečky V₁a V₂ pomocí konvexní kombinace vrcholů V₁a V₂ (koeficienty k₁ = 0.5, k₂ = 0.5).
Jaké souřadnice má vrchol, ve kterém nabývá účelová funkce svého minima?

9. Podívejte se na obrázek 2.5.; za předpokladu, že na osách x₁a x₂je měřítko 1 cm určete:

Jakou rovnici má přímka z_min!
Zvolte v příkladě další omezující podmínku tak, aby model měl řešení a účelová funkce z_max dosahovala hodnoty alespoň 100!

10. Platí-li v modelu LP podmínka nezápornosti, jaké nejmenší hodnoty může nabýt účelová funkce při minimalizaci?

2.3.7 Základní věta lineárního programování

Účelová funkce v modelu lineárního programování nabývá svého extrému na hranici konvexní množiny přípustných řešení (ve vrcholu konvexního polyedru).

Matematický důkaz věty je značně obtížný, proto jej neuvádíme. Vlastnost je ale zřejmá z postupu při grafickém řešení.

Na základě základní věty LP je možno optimální řešení modelu LP vybírat z konečného počtu řešení: model LP má konečný počet omezujících podmínek a konvexní množina přípustných řešení má proto konečný počet vrcholů. V jednom z vrcholů je hledané řešení.

2.4 Shrnutí

Lineární programování je nejpoužívanějším typem optimalizačních úloh. Tyto úlohy jsou charakteristické tím, že se z množiny přípustných variant řešení pomocí vhodně zvolené metody vybírá řešení, které se z hlediska daných podmínek a zvoleného optimalizačního kritéria jeví jako nejvýhodnější (optimální). Proto lze LP považovat za jeden z nástrojů optimálního rozhodování.

Lineární modely zobrazují systém s určitou mírou nepřesnosti, vyplývající z předpokladu linearity zobrazovaných procesů a deterministického charakteru parametrů modelu. Přesto ale poskytují důležité informace pro podporu rozhodování. Pro svoji jednoduchost a širokou použitelnost se LP stalo jednou z nejrozšířenějších metod využívaných při manažerském rozhodování.

Grafické řešení úlohy LP je založeno na geometrické interpretaci lineárních nerovnic a vlastnostech konvexních množin. Grafické řešení je omezeno na modely LP se dvěma proměnnými a konečným počtem omezujících podmínek. Grafická metoda má především didaktický význam.

2.5 Klíčová slova

Lineární programování, alokační problém, účelová (kriteriální) funkce, omezující podmínky, vektor proměnných, vektor cen, matice soustavy omezujících podmínek, verbální model, model LP, standardní tvar úlohy LP, grafická metoda řešení modelu LP, konvexní polyedr, optimální řešení, množina přípustných řešení, základní věta LP.

2.6 Otázky ke studiu