
In linear programming, a single objective is maximized or minimized subject to constraints. In many important problems, particularly in the public sector, there are several objectives that the decision maker is trying to achieve. We now consider incorporating these multiple objectives in linear programming.
Consider, as an example, the manager of a farm. State law may specify the maximum amount of nitrogen fertilizers to be used per one hectare of arable land, i.e. maximum soil contamination of nitrogen. Our manager must manage the farm so as to enhance grain, potato and milk production, cover food for dairy cows, minimize the soil contamination of nitrogen and do this at as low a cost as possible.
Suppose our manager has six activities that can be undertaken. Let:
|
|
[ha] |
[ha] |
[ha] |
[ha] |
[pcs] |
[l] |
RHS
|
|
| arable land |
|
|
|
|
30
|
|||
| acreage of wheat |
|
|
8
|
|||||
| acreage of potato |
|
|
10
|
|||||
| acreage of grassland |
|
|
15
|
|||||
| balance of food |
|
|
|
0
|
||||
| stable capacity |
|
|
30
|
|||||
| balance of milk |
|
|
|
0
|
Table 4.1 "Constraints in the Farm Production Model"
In addition, each activity has a cost – to be minimized,
some of them contaminates soil by nitrogen – this contamination has to
be minimized too, and some of them produces revenues (in terms of sold
grain, potato and milk) – to be maximized. Off course that the total benefit
must be as high as possible accepting the soil contamination to be as low
as possible. Each of these three objectives can be described separately
using one linear
programming model objective function, but our two goals (benefit maximization
and contamination minimization) will not be satisfied simultaneously! The
manager should achieve as high benefit as possible and should contaminate
the soil as low as possible. She has three objectives, three criteria functions
as shown in Table 4.2.
|
|
[ha] |
[ha] |
[ha] |
[ha] |
[pcs] |
[1000l] |
|
|
| costs |
4
|
3,5
|
6,6
|
9
|
4
|
minn
|
||
| revenues |
12
|
7,5
|
18,8
|
5
|
max
|
|||
| N contamination |
25
|
8
|
3
|
40
|
min
|
Table 4.2 "Criteria Functions in the Farm Production Model"
Joining constraints and criteria functions together we obtain mathematical model of multi criteria linear programming problem.
As shown in Table 4.2, farmer’s costs per one hectare of wheat is $400, of barley $350 etc., farmer’s revenues per one hectare of wheat is $1200, of barley $750 etc. and soil contamination for per one hectare of potatoes is 3 units.
The decision problem for the farmer is to determine x = (x1, x2, x3, x4, x5, x6) that is
how many hectares of wheat (x1), barley (x2) and potato (x3)to crop, how many hectares of soil to let for grassland (x4), how many peaces of dairy cows to breed (x5) and how much milk to produce (x6) to
a) minimize the sum of all costs – criteria function 1:
b) maximize the sum of revenues – criteria function 2:
12x1 + 7,5x2 +18,8x3 + 5x6,
c) minimize the soil contamination – criteria function 3:
25x1 + 8x2 + 3x3 + 40x5.

Remarks:
1) Balance of food - each hectare of grassland produces 29 tones of food (pasturage),each dairy cow consumes 25,5 tones of this food per year and no food can be purchased.
2) Each dairy cows produces 4 000 liters of milk per year
Three goals are to be satisfied simultaneously. There are several approaches for incorporating all these multiple objectives; we describe each in turn.
4.1 Partial Optimization
The manager may study behaviour of his/her model when only one objective is selected and all others will be ignored. The problem then becomes an ordinary linear programming problem of maximizing (minimizing) an objective function subject to constraints. Such partial solutions will be only established into other objectives. After solving three single objective LP models (using Linkosa software – see SW download) we obtain following results - see Table 4.3.
|
|
|
||||||||
|
|
[ha] |
[ha] |
[ha] |
[ha] |
[pcs] |
[ l ] |
[100$] |
[100$] |
[units] |
|
Cost |
|
|
|
|
|
|
|
|
|
|
Revenues |
|
|
|
|
|
|
|
|
|
|
Contamination |
|
|
|
|
|
|
|
|
|
Table 4.3 "Partial Optimal Solutions of the Farm Production Model"
4.2 Single Objective with Others as Constraints
The manager may decide that one objective is of such importance that it override the others. The other objectives may be built in as constraints at some minimal (maximal) level. The problem then becomes an ordinary linear programming problem of maximizing (minimizing) an objective function subject to constraints. For example, our manager may decide that cost minimization is most important for him/her.
12x1 + 7,5x2 +18,8x3 + 5x6 => 600
25x1 + 8x2 + 3x3 + 40x5 <= 500 .
| Optimal Solution of the Model FARM PRODUCTION | ||||||
| Min. value of the objective function "costs" | ||||||
|
231,0503448
|
||||||
| Structural variables | Constraints | |||||
|
|
|
|
|
|
|
|
| wheat[ha] |
8
|
Basic | arable land |
30
|
0
|
|
| barley[ha] |
0
|
Lower bound | acreage of wheat |
8
|
0
|
|
| potato[ha] |
22
|
Basic | acreage of potato |
10
|
-12
|
|
| grassland[ha] |
3,97
|
Basic | acreage of grassland |
15
|
11
|
|
| cows[pcs] |
4,52
|
Basic | balance of food |
0
|
0
|
|
| milk[1000 l] |
18,08
|
Basic | stable capacity |
30
|
25,48
|
|
| balance of milk |
0
|
0
|
||||
| revenues |
600
|
0
|
||||
| N contamination |
500
|
53,2
|
||||
Analyzing optimal solution as shown in Table 4.4 we can see, that the farmer’s cost will be $23 100, revenues will be exactly $60 000 (his/her minimum demand) and the N contamination will not exceed 500 units (it will even be only 500 - 53,2 = 446,8).
Analyzing the sensitivity analysis (odkaz do LP) values of the model solution the manager can for example restrict the nitrogen contamination to be at most 300 units
25x1 + 8x2 + 3x3 + 40x5 <= 300 .
12x1 + 7,5x2 +18,8x3 + 5x6 =>500
| Optimal Solution of the Model FARM PRODUCTION | ||||||
| Min. value of the objective function ”costs” | ||||||
|
173,53
|
||||||
| Structural variables | Constraints | |||||
|
|
Value | Type | Name | Value | Slack | |
| wheat[ha] |
|
|
arable land |
|
|
|
| barley[ha] |
|
|
acreage of wheat |
|
|
|
| potato[ha] |
|
|
acreage of potato |
|
|
|
| grassland[ha] |
|
|
acreage of grassland |
|
|
|
| cows[pcs] |
|
|
balance of food |
|
|
|
| milk[1000 l] |
|
|
stable capacity |
|
|
|
| balance of milk |
|
|
||||
| revenues |
|
|
||||
| N contamination |
|
|
||||
For another example, our manager is an ecologically thinking man and so s/he may decide that N Contamination overrides all other criteria. Such approach will guide him/her to a ” Farm Production Model with Costs and Revenues as Constraints” in principle very similar to the model mentioned above.
4.3 Goal Programming
A third approach is that of goal programming. The decision maker specifies desirable goals for each objective. Then the problem is formulated so as to minimize the shortfall related to obtaining these goals. The goals are usually specified at desirable
(high) levels, so that it is not possible to satisfy all simultaneously.
Suppose the manager in our example set as desirable goals the costs $20000, the revenues $50000 and the N contamination 350 units. The constraints derived from the goal programming mathematical model then become
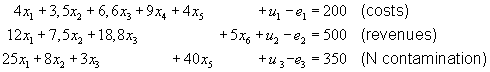
The variables uk represent the amounts by which the plan fails to achieve the goals. Thus, these can be described as the shortfall or underage. The variable u1represents saving in dollars below the maximum costs level, the variable u2represents underachievement of revenues and the variable u3 represents saving in units below the maximum defined N contamination of soil.
The variables ek represent the amounts by which the specified goals are exceeded—that is, the overage. The variable e1 represents overbudgeting in dollars, the variable e2 represents overachievement of demanded revenues and the variable e3 represents how much the maximum defined N contamination of soil is exceeded.
One method of forming the objective function in goal programming is to minimize goals underachievement (in case of maximization) and overachievement (in case of minimization). In our case e1 + u2 + e3. Let’s set the goals to the ideal values (see vector h above). This would minimize the amounts by which costs and contamination are exceeded and by which the revenues are not reached. The simplicity of this approach is appealing. But there is a major assumption, that one unit savings in dollars (costs compared to revenues) has the same value as a unit shortfall in N contamination. The objective function has given equal weight to each.
A better approach is to define specifically the trade-offs among the various objectives. Suppose our manager decides that 100 dollar savings in costs is 10 times more important, and every 100 dollars revenues more is 5 times more important that one unit of N contamination above its limit. Then the objective function would be:
The manager might decide that there is some value to overages in case of maximization goals and attach weights to their e variables too. Or s/he might decide that there is some value to underachievement of minimization goals and attach weights to the their u variables too. This way we obtain a full goal programming mathematical model. For example, each $100 of exceeding the goal of revenue may be 5 times more important than one unit of N contamination overrun and so on.
In case of more sophisticated goal programming models the weights of goals under(over)achievement are to be normalized.
Farm Production Goal Programming Model – Approach B shows us the solution of our model, where the farmer sets as desirable goals the costs $15000, the revenues $60000 and the N contamination 300 units (see model formulation above in this chapter) All these goals can be overachieved or underachieved, all weights are normalized.
4.4 Trade-Offs Among Objectives – Aggregation of Objective Functions
Last mentioned approach to multi objective problems is to specify the trade-offs among the objectives using a method of objective functions aggregation. In the present example our farmer would specify how much N contamination minimization is important in comparison with cost minimization and how much cost minimization is important in comparison with revenue maximization. There is a lot of principles of how to compare these importance of objectives and how to aggregate them into a single one. In the new objective function all former objectives must save their weight. One possibility of how to join all criteria into a single one is to assign normalized weights (the method of weights normalization is very similar to the goal programming approach) to each objective function, to multiply them by these weight and to sum them into a single objective function. The problem then becomes an ordinary linear programming problem of maximizing (minimizing) one objective function subject to constraints. It is very important, that all former criteria functions must be of the same type (either max or min). If no, the decision maker must choose the type of final criteria function - e.g. max, and to multiply all former minimization criteria by the value of (-1). The new objective function achieved after criteria functions aggregation is only auxiliary and its max (min) value has no meaningful sense. The optimal solution values must be established into former criteria functions to obtain the real criteria values.
Our farmer may specify the ratio of objective importance to 2 : 2 : 1. It means, that the cost minimization is equally important to revenue maximization and both these criteria are twice more important than N contamination minimization. Respecting this ratio objective functions normalized weights will be set to 2/5, 2/5 and 1/5. The final aggregated objective function then becomes:
![]()
Note that the first and second criteria function were multiplied by (-1) because former objectives were of the minimization type and the final aggregated function is of the maximization type.
After rearrangement our problem can be expressed as:

Solving this problem using Linkosa software
we obtain following optimal solution:
| Optimal Solution of the Model Farm Production | ||||||
| Max. value of the objective function Z - aggregated | ||||||
|
79,76
|
||||||
| Structural variables | Constraints | |||||
| Name | Value | Type | Name | Value | Slack | |
| wheat [ha] |
8
|
Basic | arable land |
30
|
0
|
|
| barley [ha] |
0
|
Lower bound | acreage of wheat |
8
|
0
|
|
| potato [ha] |
22
|
Basic | acreage of potato |
10
|
-12
|
|
| grassland [ha] |
0
|
Lower bound | acreage of grassland |
15
|
15
|
|
| cows [pcs] |
0
|
Lower bound | balance of food |
0
|
0
|
|
| milk [l] |
0
|
Basic | stable capacity |
30
|
30
|
|
| balance of milk |
0
|
0
|
||||
Table .1" Optimal Solution of the Farm Production Model with Weighted Criteria Aggregation"
Costs = $17 720Comparing these values with ideal and nadir ones we can see that they are quite favorable and it means that our weights were set correctly.
Revenues = $50 960
N contamination = 266 units.
4.5 Conclusion
There are several methods of incorporating
multiple objectives in linear programming problems. Simple approaches involve
converting to a single-objective function by weighting the objectives or
by incorporating the secondary objectives as constraints. Goal programming
involves defining goals and including variables for deviations from these
goals (either shortfalls or excesses). The objective function is defined
to minimize the (possibly weighted) deviations. We can observe that goal
programming differs from all other approaches because the objective function
is defined in terms of the objectives themselves. The goal programming
approach makes it easier to see the relative value attached to each of
the multiple objectives.