
9.1 What is a "Queue "
Any system where jobs (or customers, users) arrive looking for service and depart once service is provided. A schematic of a typical queue is shown below:

9.1.1 Some Examples Where we Encounter Queuing
9.1.2 Modelling Issues and Performance
Queuing theory or waiting line theory is primarily concerned with processes characterised by random arrivals (i.e., arrivals at random time intervals); the servicing of the customer is also a random process. If we assume there are costs associated with waiting in line, and if there are costs of adding more channels (i.e., adding more service facilities), we want to minimise the sum of the costs of waiting and the costs of providing service facilities. The computations will lead to such measures as the expected number of people in line, the expected waiting time of the arrivals, and the expected percentage utilisation of the service facilities. These measures can then be used in the cost computations to determine the number and capacity of service facilities that are desirable.
a) Most frequent modelling issues in the study of queues and queuing:
Arrival Process Description.
How does one describe the process of customer
arrivals?
Buffer Size/lNumber of Waiting Positions.
Is there any provision to wait in the queue in
case the server(s) are currently busy?
Service Discipline.
Are there any local rules governing the order
in which service is provided and/or the type of service?
Service Time Distribution.
What is the length of service and what is its
distribution if this is a random variable?
Priorities.
Are there any service priorities involved which
decides between customers on who should be serviced first?
b) Most frequent performance issues in the study of queues and queuing:
Mean Service Parameters such as mean waiting times, mean number in queue etc..
Distribution of Service Parameters or their transforms - much harder to find usually than the means but would be nice to know them, if possible.
Server utilisation.
Number and distribution of customers leaving without service, if any.
Description of the customer departure process - usually very hard to find.
9.1.3 Economics of the Waiting Line Problem
Understanding waiting lines or queues and learning how to manage them is one of the most important areas in operations management. It is basic to creating schedules, job design, inventory levels, and so on. In our service economy we wait in line every day, from driving to work to checking out at the supermarket. We also encounter waiting lines at factories-jobs wait in lines to be worked on at different machines, and machines themselves wait their turn to be overhauled. In short, waiting lines are pervasive.
In this section we discuss the basic elements concerning economics and decision making of waiting line problems and provide standard steady-state formulas for solving them. These formulas, arrived at through queuing theory, enable economists and planners to analyse service requirements and establish service facilities appropriate to stated conditions. Queuing theory is broad enough to cover such dissimilar delays as those encountered by customers in a shopping mall or aircraft in a holding pattern awaiting landing slots.
The central problem in virtually every waiting line situation is a trade-off decision. The manager must weigh the added cost of providing more rapid service (more traffic lanes, additional landing strips, more checkout stands) against the inherent cost of waiting.
Frequently the cost trade-off decision is straightforward. For example, if we find that the total time our employees spend in line waiting to use a copying machine would otherwise be spent in productive activities, we could compare the cost of installing one additional machine to the value of employee time saved. The decision could then be reduced to dollar terms and the choice easily made.
On the other hand, suppose that our waiting line problem centres on demand for beds in a hospital. We can compute the cost of additional beds by summing the costs for building construction, additional equipment required, and increased maintenance. But what is on the other side of the scale? Here we are confronted with the problem of trying to place a dollar figure on a patient's need for a hospital bed that is unavailable. While we can estimate lost hospital income, what about the human cost arising from this lack of adequate hospital care?
Figure 1 shows the essential trade-off relationship under typical (steady-state) customer traffic conditions. Initially, with minimal service capacity, the waiting line cost is maximum. As service capacity is increased, there is a reduction in the number of customers in the line and in their waiting times, which decreases waiting line cost.
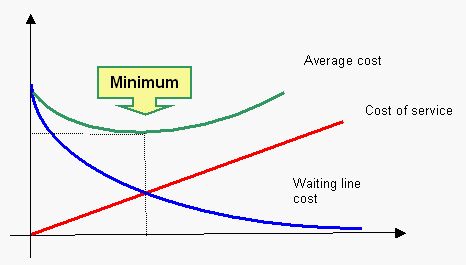
Figure 1
9.1.4 Finite and Infinite Population in Queues
Arrivals at a service system may be drawn from a finite or an infinite population. The distinction is important because the analyses are based on different premises and require different equations for their solution.
Finite Population: A finite population refers to the limited size customer pool that will use the service and, at times, form a line. The reason this finite classification is important is because when a customer leaves its position as a member of the population of users (by a machine breaking down and requiring service, for example), the size of the user group is therefore reduced by one, which reduces the probability of the next occurrence. Conversely, when a customer is serviced and returns to the user group, the population increases and the probability of a user requiring service also increases. This finite class of problems requires a separate set of formulas from that of the infinite population case. See an Example of a finite population.
Infinite Population: An infinite population is one large enough in relation to the service system so that the changes in the population size caused by subtractions or additions to the population (a customer needing service or a serviced customer returning to the population) does not significantly affect the system probabilities. See an Example of an infinite population .
9.1.5 Queues and Waiting Lines in Everyday Life
Queues or waiting lines are very common in everyday life. There are few individuals in modem society who have not had to wait in line for a bus, a taxi, a movie ticket, a grocery check out, a haircut, or registration material at the beginning of the school year. Most of us consider lines an unavoidable part of our civilised life, and we put up with them with more or less good humour. Occasionally, the size of a line we encounter discourages us, we abandon the project, and a sale is lost.
9.1.6 Management of Queues
Fortunately for the busy manager, reasonable queuing decisions can frequently be based on past experience or on the facts of the current situation. Thus, the management of a grocery chain knows approximately how many check out counters should be installed in a new store by looking at the experience of comparable stores. At any time of the day, the store manager can tell how many of the installed counters should be open by noting the lengths of the queues and adding personnel from other chores, or sending the present checkout personnel to other tasks. Also, historical records (for example of machine downtime) can indicate the amount of time that machines had to queue for repairs rather than relying upon the computations resulting from a mathematical model to determine the amount of downtime.
Although a number of problems encountered by an executive can be reasonably solved by the use of intuition or past experience, there will be many situations that are too complex for our intuition or where we desire a more accurate answer than we can expect to be supplied by intuition. In these situations, the problem can be approached by either simulation or a mathematical model procedure.
9.2 Mathematical Modelling of Queuing
9.2.1 Background to the Solution
There are two approaches to mathematical analysis
of a queue:
1. Analytical model. Behaviour of all elements
in the queue is described by system of (differential) equations.
2. Simulation model. Behaviour and relations
among elements of the queue is modelled by computer programme.
In this section we describe in detail two models: a) the single-channel and b) the multiple-channel, both with infinite source and patient customers. These two types of queues might be thought of as the mainstream queuing models - this stems partly from the ease understanding of queuing systems that they convey and partly from the ease with which system performance measures can be obtained.
However, the field of queuing contains a rich variety of models - all these models can be solved as a slight or complicated variations in the assumptions which underlie the two basic models above.
Other queuing models one can solve using special SW for queues or by means of simulations.
In both analytical and simulation model there are four major elements of any queuing situation which must be considered: arrivals, services, number of servers, queue discipline.
9.2.2 Arrivals
Customers come into the system for service. How these customers arrive in the system is important:
When describing a waiting system, we need to define the manner in which customers or the waiting units are arranged for service.
Waiting line formulas generally require an arrival rate, or the number of units per period (such as 10 units per hour). The time between arrivals is the interarrival time (such as an average of one every six minutes). A constant arrival distribution is periodic, with exactly the same time period between successive arrivals. In productive systems, about the only arrivals that truly approach a constant interarrival period are those that are subject to machine control. Much more common are variable (random) arrival distributions.
In observing arrivals at a service facility, we can look at them from two viewpoints: We can analyse the time between successive arrivals to see if the times follow some statistical distribution. Usually, we assume that the time between arrivals is exponentially distributed. We can set some time length (t) and try to determine how many arrivals might enter the system within t. We will typically assume that the number of arrivals per time unit is Poisson distributed. See Exponential distribution.
9.2.4 Other Arrival Characteristics – Patterns, Size, Patience
Other arrival characteristics include arrival patterns, size of arrival units, and degree of patience:
Arrival patterns: The arrivals at a system are far more controllable than is generally recognized. Barbers may decrease their Saturday arrival rate (and supposedly shift it to other days of the week) by charging an extra $1 for adult haircuts or charging adult prices for children's haircuts. Department stores run sales during the off-season or hold one day-only sales in part for purposes of control. Airlines offer excursion and off-season rates for similar reasons. The simplest of all arrival-control devices is the posting of business hours.
Some service demands are clearly uncontrollable, such as emergency medical demands on a city's hospital facilities. But even in these situations, arrivals at emergency rooms in specific hospitals are controllable to some extent by, say, keeping ambulance drivers in the service region informed of the status of their respective host hospitals.
Size of arrival units: A single arrival may be thought of as one unit. (A unit is the smallest number handled.) A single arrival on the floor of the New York Stock Exchange is 100 shares of stock; a single arrival at an egg-processing plant might be a dozen eggs or a flat of 2t/2 dozen; or a single person at a restaurant.
A batch arrival: It is some multiple of the unit, as a block of 1,000 shares on the NYSE, a case of eggs at the processing plant, or a party of five at a restaurant.
Degree of patience: A patient arrival is one who waits as long as necessary until the service facility is ready to serve him or her. (Even if arrivals grumble and behave impatiently, the fact that they wait is sufficient to label them as patient arrivals for purposes of waiting line theory.)
There are two classes of impatient arrivals. Members of the first class at TGV, survey both the service facility and the length of the line, and then decide to leave. Those in the second class arrive, view the situation, join the waiting line, and then, after some period of time, depart. The behaviour of the first type is termed balking, while the second is termed reneging.
9.2.5 Queue and Services
The queuing system consists primarily of the waiting lines and the available number of servers. Factors to consider here include the line length, number of lines, and queue discipline. Each customer must be serviced. How long it takes to complete a service is the second important element. It may take the same time for each customer, or service times may vary considerably in a random fashion.
There may be only one server or channel or many servers. A customer may be processed by only one server or several in turn. Servers may have different service rates.
Length: In a practical sense, an infinite line is very long in terms of the of the service system. Examples of infinite potential length are a line of vehicles backed up for miles at a bridge crossing and customers who must form a line around the block as they wait to purchase tickets at a theatre.
Gas stations, loading docks, and parking lots have limited line capacity caused by legal restrictions or physical space characteristics. This complicates the waiting line problem not only in service system utilization and waiting line computations but also in the shape of the actual arrival distribution. The arrival denied entry into the line because of lack of space may rejoin, the population for a later try or may seek service elsewhere. Either action makes an obvious difference in the finite population case.
Number of lines: A single line is one line only. The term multiple lines refers either to the single lines that form in front of two or more servers onto single lines that converge at some central redistribution point. The disadvantage of multiple lines in a busy facility is that arrivals often shift lines if several previous services have been of short duration or if those customers currently in other lines appear to require a short service time.
9.2.6 Service Time Distribution
Another important feature of the waiting structure is the time the customer or unit spends with the server once the service has started. Waiting line formulas generally specify service rateas the capacity of the server in number of units per time period (such as 12 completions per hour) and not as service time, which might average five minutes each. A constant service time rule states that each service takes exactly the same time. As in constant arrivals, this characteristic is generally limited to machine-controlled operations.
When service times are random, a good approximation
of them can be given by the exponential
distribution . When using the exponential distribution as an approximation
of the service times, we will refer to ![]() ,
as the average number of units or customers that can be served per time
period.
,
as the average number of units or customers that can be served per time
period.
9.2.7 Line Structures
The flow of items to be serviced may go through a single line, multiple lines, or some mixtures of the two. The choice of format depends partly on the volume of customers served and partly on the restrictions imposed by sequential requirements governing the order in which service must be performed.
The simplest type of waiting line structure is single server, single phase, and straightforward formulas are available to solve the problem for standard distribution patterns of arrival and service. When the distributions are non standard, the problem is easily solved by computer simulation. A typical example of a single server, single phase situation is the one-person barbershop.
9.2.8 Queue Discipline
While customers wait for service, they are in a waiting line or queue. There may be only one line or separate ones for each server. There may be a space limit on the waiting line, and customers who arrive when the line is full may turn away called balking.
Queue discipline: A queue discipline is a priority rule or set of rules for determining the order of service to customers in a waiting line. The rules selected can have a dramatic effect on the system's overall performance. The number of customers in line, the average waiting time, the range of variability in waiting time, and the efficiency of the service facility are just a few of the factors affected by the choice of priority rules.
Probably the most common priority rule is first come, first served (FCFS). This rule states that customers in line are served on the basis of their chronological arrival; no other characteristics have any bearing on the selection process. This is popularly accepted as the fairest rule although in practice, it discriminates against the arrival requiring a short service time.
Reservations first, emergencies first, highest profit customer first, largest orders first, best customers first, longest waiting time in line, and soonest promised date are other examples of priority rules. There are two major practical problems in using any rule: One is ensuring that customers know and follow the rule. The other is ensuring that a system exists to enable the employees to manage the line (e.g., take-a-number systems).
9.3 Measures of Performance
There are various ways of judging how well a queuing system is performing. Results may be evaluated over a short period of time once the system opens, or based on the long run or equilibrium results.
A given queuing system can have any combination of the elements described above. Hence, there are a very large number of possible systems, and no one mathematical model can describe them all. In this section, we focus on a few simple models that have wide applicability, and that give us insight into queuing system behaviour in general. Most queuing systems behave like the cases examined in this chapter.
There are various ways of judging how well a processing system is performing. Results may be evaluated over a short period of time once the system opens, or they may be based on the long-run or equilibrium results. Generally, the time jobs spend waiting is important, and we may look at the average waiting time or at a measure such as the percent of jobs that wait longer than, say, 10 minutes. A related measure is the throughput time for a job (waiting time plus service time). The length of the waiting line is another common measure of performance. These are measures of how well the system is performing from the customer point of view.
Other measures relate to the cost of operating the system. The system load factor or capacity utilisation measures the ability of the system to handle the arrival load. Management has the option of adding more capacity.
9.4 Modelling of Random Relations in the Queue
There are two important probability distributions that appear often in queuing models. The Poisson distribution assumes a very large (infinite) number of possible arrivals, with each having a small probability of occurrence. Arrivals are independent and the number of arrivals in one period of time does not affect the number in the next. The Poisson distribution is a good approximation for many processes that are considered "random," such as calls arriving at a switchboard, customers at a check-in counter, or fire alarms.
The random variable in the Poisson distribution is the number of events (e.g., arrivals) in a unit of time. The exponential distribution is a complementary distribution to the Poisson that has as the random variable the time between events. Both of these distributions are called Markov distributions.
9.5 A Single-Server Queuing Model
9.5.1 Kendall´s Notation for Queues
Kendall's notation for queues is a useful way to represent different types of queues in a compact and easily understood their fashion. Kendall's notation describes:
1. nature of the arrival process to the queueThe notation has been considerably extended to allow it to represent a wide variety of queues.
2. nature of the service time
3. number of servers
4. maximum number customers in the queue
5. queuing disciplines (behaviour of customers in the queue)
Following this representation, a queue is represented by a sequence
X/Y/k/Q/D
with the following meaning attached to the letters A to E:

"X" symbolically represents the nature of the arrival process to the queue. Special letters are used to symbolise the nature of the interarrival time distribution as follows:
M Exponentially distributed interarrival times (Poisson Process, Markov Process)
D Deterministic (fixed) inter-arrival times
Ek Erlang distribution of order k for the inter-arrival times
Hk Hyper-exponential distribution of order k for the inter-arrival times
G General (any!) distribution for the inter-arrival times
etc.

"Y" symbolically represents the nature of the service time distribution for the customers getting served in the queue. The same letters as the ones above are used to describe the nature of the service time distribution.


"Q" Maximum number of customers that can be there in the queue - this includes both the ones currently being served and the ones waiting for service. Default is infinity many which is assumed when this is omitted.

FCFS First Come First Served9.5.2 Example
LCFS Last Come First Served
SIRO Service in random order
etc.
M/M/1
Poisson Arrivals, Exponential Service
Time Distribution, Single Server, Infinite Number of Waiting Positions
M/Ez/2/K
Poisson Arrivals, Erlangian of order-2
Service Time Distribution, 2 Severs, Maximum Number K in queue
G/M/2
Generalised Arrivals, Exponential Service
Time Distribution, 2 Servers, Infinite Number of Waiting Positions
9.6 Mathematical Model of M/M/1 System
9.6.1 Model Description
1. Arrivals are random, and come from the Poisson probability distribution (Markov impute).9.6.2 Notation
2. Each service time is also assumed to be a random variable following the exponential distribution (Markov service).
3. Service times are assumed to be independent of each other and independent of the arrival process.
4. There is one single server in the queue.
5. The queue discipline is FIFO, and there is no limit on the size of the line.
6. The average arrival and service rates do not change over time. The process has been operating long enough to remove effects of the initial conditions.
|
|
Average number of customers arriving in one unit of time |
|
|
Average number of customers the facility is capable of servicing in one unit of time, assuming no shortage of customers |
|
|
Expected number of units being serviced and/or waiting in the system |
|
|
Expected number in the queue (the number in the queue does not include the unit being serviced) |
|
|
Probability of having n units in the system |
|
|
Expected time an arrival must wait in the queue |
|
|
Expected time an arrival spends in the system (both in queue and in service) |
System must be operating long enough so that the probabilities resulting from the physical characteristics of the problem may satisfy the requirements of the mass selection of a statistical observation - that is, the system must be in equilibrium.
Define ![]() as an utilisation of the system and suppose r
< 1. There are following relationships of interest:
as an utilisation of the system and suppose r
< 1. There are following relationships of interest:
1. Probability that there are n arrivals in the system (in case of system M/M/1 there is one arrival in the service channel and the rest n -1 arrivals are waiting in the queue):
pn = rn(1 - r )
2. Probability of the system being empty - expected idle time of the system:
p0 = (1 - r )
3. Probability of the system being not empty - expected busy time of the system or expected utilisation:
1 - p0 = r
4. The expected number in the waiting line and/or being serviced is:
![]()
5. The expected number in the queue is:
![]()
6. The average waiting time (in the queue) of an arrival is:
![]()
7. The average time an arrival spends in the system (both waiting and in service) is:
W = Wq + 1/µ
The probability that the number in the queue and being serviced is greater than M is:
P{n >M} = ![]()
9.6.4 Example
Analyse system of queue in an office. Population of customers is very large so that we can consider it is an infinite one). Customers for the service arrive randomly following a Poisson process. The office can process customers at an average rate of five patients an hour (one at a 12 minutes).The service process is also Poisson. Customers are served at an average of four per hour (one at a 15 minutes). The office operates 12 hours a day.
First, all measures assume the process has been operating long enough for the probabilities resulting from the physical characteristics of the problem to have made themselves felt; that is, the system is in equilibrium.
Second, the utilisation of the system is r= ![]() /µ
= 4/5 = 0,8 < 1, thus we can count relationships as follows:
/µ
= 4/5 = 0,8 < 1, thus we can count relationships as follows:
1) Probability of the system being empty - expected idle time of the system:
p0 = (1 - r ) = 1 - 0,8 = 0,2
On average, the office will be idle 20 percent of the time and busy 80 percent of the time.
2) The expected number in the system - both in waiting line and being serviced is:
![]() =
= ![]() = 4
= 4
There will be an average of four persons in line and being serviced.
3) The expected number in the waiting line is:
![]() =
= ![]()
There will be an average of 3,2 people in waiting line.
4) The average waiting time (in the queue) of an arrival is:
![]()
The average waiting time of an customer is 0,8 of an hour (e.g. 48 minutes).
5) The average time an arrival spends in the system (both waiting and in service) is:
W = Wq + 1/µ = 0,8 + 1/5 = 1
The average time spent in the system - both in the waiting line and obtaining service - is one hour.
If we assume a 12 hour workday, there will be an average of 48 customers arriving per day, and the expected total lost time of customers waiting will be:
T =![]() .12. Wq = 4.12.0,8 = 38,4.
.12. Wq = 4.12.0,8 = 38,4.
There will be a cost associated with these 38,4 hours. Assume the cost to the society is $10 for each hour lost by a customer waiting. The average cost per day from waiting is
38,4.10 = $384
Suppose that we could in some fashion increase the service rate from five to six per hour and thereby decrease the average time spent in service from 12 minutes to 10 minutes. What would be the effect of this change?
With µ = 6, the expected number in the queue is
![]() =
= ![]()
instead of the 3.2 found above. The average wait for the patient is now:
![]() (of an hour).
(of an hour).
Before the change, each customer spent an average of 12 minutes being served and 48 minutes waiting. After the change, each patient will spend an average of 10 minutes being served, and 20 minutes waiting. This can be verified by computing the total time in the system:
W = Wq + 1/µ = 1/3 + 1/6 = 1/2 (of an hour).
Each day there are 48 customers (4.12), and each customer will save one-half hour in total. At a cost of $10 per hour, the daily cost savings is:
48.1/2.20 = $480.
It would be worth $480 per day or $175200 per year to the society to increase the service rate to six customers at office per hour.
9.6.5 Queuing System Behaviour
The formulas presented for the single system M/M/1
case enable us to study system behaviour as the arrival rate ![]() approaches the service rate µ. Recalling that
approaches the service rate µ. Recalling that
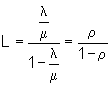
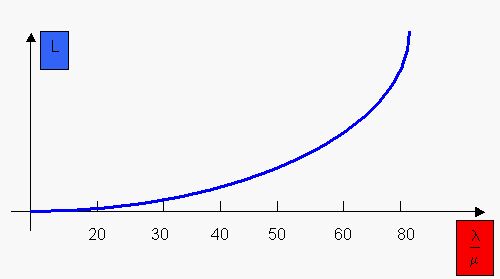
Figure 1
Figure 1 shows how responsive the number in the system
L is to the utilisation r
. In a single queuing system M/M1 as the utilisation r
rises much above 80 percent, the expected number L in the system rises
ever
more sharply. The general implication is that if prompt service is
desired in a single channel system, there must be parameter ![]() much less then parameter µ in order to avoid excessive waiting.
much less then parameter µ in order to avoid excessive waiting.
Although Figure 1 is directly applicable only under the stated assumptions, it is striking how many business situations behave in a qualitatively similar manner when utilisation changes. Even in complex production facilities with many machines and alternative routings for parts, it has often been observed that when increased demand leads to an increase in shop utilisation, there is an even greater increase in the time an order spends in the shop (waiting time plus time being processed), fitting the general pattern of Figure 1.
There is pressure in most organisations to be efficient and to reduce idle time as much as possible. Managers do not like to see personnel or equipment standing idle. Yet with random arrivals and service times, we see the need to have excess capacity to avoid long lines and long waits for customers. This is a very important insight about queuing systems and one that is not obvious to most people.
9.6.6 How to Analyse Random Data
Suppose you are operating a system in which customers arrive in random (Markov) process. Table 1 shows a history of 30 arrivals over a period of about eight hours. The left part of the table shows the actual times of arrival, when the customers actually started service, and when they were finished. The numbers at the right are calculated from these data: the length of waiting line ahead of the arrival, the interarrival time, the actual time taken to service the patient, and the amount of time each patient spent waiting.
Note that there is considerably variability in arrival patterns and in service time needed.
For example, seven customers arrived in the hour between 13:00 to 14:00 (1 to 2 p.m.) and yet there was only one arrival in the hour between 10:00 and 11:00. Similarly, some customers needed only 6 or 7 minutes of service time, while one patient took 19 minutes.
As can be seen, the first arrivals had zero or short waits. However, after customer number 11, the line and waiting times began to build up. Several arrivals had to wait more than 50 minutes, and the waiting line built up to as many as 6 customers by the time customer 26 arrived. But the line shortened again, so that customer number 30 had a short wait.
In the table one can see patterns that are typical in most queuing systems. There is variability in the interarrival times and in the service times for customers, and this results in lines and waits for service. Note that while the average waiting time was 28,4 minutes, this number doesn't fully capture the waiting time pattern. Eight of the 30 arrivals had to wait 50 minutes or more, and three people an hour or more.
In terms of service capacity, note that the table covered a period of 474 minutes. The average service time was 12,1 minutes. Thus, the total service time for all 30 arrivals was 30*12,1 = 363 minutes. Capacity utilisation was thus 363/474 = 77 percent. The system was servicing customers only about three-fourths of the time. And yet there was substantial congestion with long waits for customers.
All data can be processed by suitable statistical
software to obtain information about distributions of arrivals and service
time (for example ”![]() -quadrate
can be used) and corresponding parameters
-quadrate
can be used) and corresponding parameters ![]() and
and ![]() .
.
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9.6.7 Example of a M/M/1 Queue
A bank wants to know how many customers are waiting for a drive-in teller, how long they have to wait, the utilisation of the teller, and what the service rate would have to be so that 95 percent of the time there will not be more than three cars in the system at any one time.
Properties of the system:
Single server, infinite population, Poisson arrivals, Exponential service pattern, unlimited queue.
Typical situations: Drive-in teller at banks, post-offices, one-lane toll bridge.
Used formulas:
1. Probability that there are n arrivals in the system pn = rn(1 - r )
2. Probability of the system being empty: p0
= (1 - r )
3. The expected number in the waiting line and/or
being serviced is: ![]()
4. The expected number in the queue is: ![]()
5. The average waiting time (in the queue) of an
arrival is: ![]()
6. The average time an arrival spends in the system
(both waiting and in service) is: W = Wq + 1/µ
Solution:
The average utilisation of the teller is ![]() = 75 percent
= 75 percent
The average number in waiting line is Lq = 2,25 customers
The average number of customers in the system is 3 customers
Average waiting time in waiting line is 0,15 hour e.g. 9 minutes
Average waiting time in the system is 0,2 hour e.g. 12 minutes.
9.7 A Multiple-Server Queuing Model
The multiple-server, or multiple-channel model, as it is sometimes referred to, is very similar to the single-server model, except that the number of servers is not limited to one.
9.7.1 Basic properties of the multiple-server model
Suppose that these conditions are satisfied:
1. A Poisson arrival rate.
2. An exponential service time.
3. There are S servers in the system.
4. The processing order is FCFS (first-come, first-served).
This can be described by Kendal classification as
system M/M/S/FCFS.
5. The calling population is infinite.
6. There is no upper limit on queue length.
7. Al servers are homogeneous - e.g. have the same
mean service rate.
9.7.2 Multi-Server Models in Practice
Multiple-channel systems are found in banks and post offices where there are single waiting lines and at bakery and deli counters where customers take a number and then are served in that order. Usually, supermarket checkouts would not fall into this category. even though they have multiple checkouts, because customers in a general way do not form a single line.
9.7.3 Multi-Server Formulas
As can be seen below, the formulas for multi-server performance measures are quite formidable, particularly for large values of S. Fortunately, there are easier methods for obtaining values: we can use a) tables or b) count the formulas in spreadsheets. The best idea is - of course - use a professional software which is available on the software market.
Following formulas are used to measure performance of the multiple-server systems:
1. System utilisation
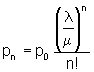

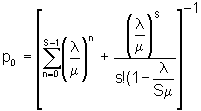
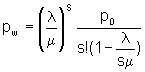
6. Average number in line
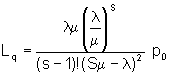
7. Average number in the system
9.7.4 Example
Management of a shop plans to open during Sundays. The shop will have three cash registers with an expected service time 1 minute, projected mean arrival rate is expected to be 1,2 customers per minute.
We shall compute basic performance measures using formulas for multiple-server model.
First, ![]() = 1,2; µ = 1,0; S = 3. The units of time will be minutes.
= 1,2; µ = 1,0; S = 3. The units of time will be minutes.
The system utilisation
Other formulas require the probability p0; according to formula 4 we get
p0 = 
Using p0 we can easy determine other measures:
 customers in the line.
customers in the line.
![]() customers in the system.
customers in the system.
![]() is average
time a customer spends in the line.
is average
time a customer spends in the line.
![]() is average
time a customer spends in the system.
is average
time a customer spends in the system.
When will a customer have to wait? The probability of this event must be Pw calculated for S = 3:
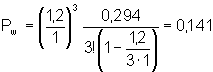 .
.
We can conclude: practically no queue exists in the system, the probability that a customer will wait is very small. System should run well.
Of course, the next step of the solution is to prove if would be possible to decrease the number of cash registers to two.
9.8 Practical experiences obtained by system modelling of queues
Adapted from: Source: K. Katz, B. M. Larson, and R. C. Larson, "Prescription for the Waiting-in-Line Blues," Sloan Management Review, Winter 1991, pp. 51-52.
1. Do not overlook the effects of perceptions management.
Consumer concern about waiting is growing. There is no limit to the frustration that waiting can cause.. Cities are becoming more crowded, the work week is expanding, the economy is worsening, and people need more free time to deal with their frustrations. Now, more then ever, excellent service is the key to success. Using perceptions management to improve customer satisfaction is only a tool, but it is a good tool.
2. Determine the acceptable waiting time for your customers.
One minute of waiting in a bank will probably go unnoticed, whereas a minute on hold on the telephone can be infuriating. Determining an acceptable waiting period will help managers set operational objectives and, if those are met, will improve customer satisfaction.
3. Install directions that entertain and physically involve the customer.
Keep the content light hearted. Piped-in music or live piano players may create a more pleasant atmosphere, but they do not effectively rope the customer into the activity. If the content of the distraction is light, fresh, and engaging, customers remain interested and entertained for many visits. Customers at the bank preferred horoscopes and tabloid headlines to more informative headline news.
The message screen used in our study managed perceptions effectively. It was inexpensive, easy to operate, and did not disrupt normal operations. Screen placement forced customers to the turn slightly in order to read it. Thus they stood shoulder to shoulder rather than front to back.
4. Get customers out of line.
Whenever customers can be served without having to stand in line, both company and customer can benefit. For example, queues can be avoided by advance reservations, by mail or telephone service, or by better automation.
5. Only make people conscious of time if they grossly overestimate waiting times.
There is a trade-of between the accuracy of waiting time perceptions and awareness of time. In the bank, perceptions were fairly close to reality, perhaps because customers had previous experience with the branch, or because the lines were short. For whatever reason, informing customers of their expected waiting time backfired. The clock made people more aware of the waiting time. It also appeared to increase balking rate.
However, there may be numerous instances in which information on expected waiting times is helpful. Airline passengers, for example, have no way of knowing when a plane sitting on the runway will take off unless they are told.
6. Modify customer arrival behaviour.
Customers are often aware of peak times before they arrive at a service location, but they show up then anyway. If some customer could be convinced to arrive at other times, everyone would be better off. To achieve this, signs what list off-peak hours could be posted in stores and banks. Servers could also mention off-peak hours to customers who have waited an inordinate amount of time. In addition, incentives could be used to encourage off-peak arrivals.
7. Keep resources not serving customers out of sight.
Several customers commented that they do not mind waiting so long as the tellers seem to be working as hard as they can. Customers tend to become annoyed it they see several unstaffed teller window or if tellers are present but not serving customers.
To address this perception, managers can adopt several policies:
The three types of customers we observed a) watchers, b) impatients, and c) neutrals want different types of service from the bank. Watchers find the bustle of the bank entertaining and prefer a friendly teller with a smile to a shorter line. The impatient group is more apt to emphasise the length of the queue in their definition of overall satisfaction.
The needs of the "impatients" can be met through innovative products, services, and educational programs that either avoid or reduce the waiting experience. The airline and hotel industries, for example, have developed club memberships that provide express check-in and check-out policies. Some retailers satisfy convenience-seeking consumers by creating express check-out cashier lines. The emergence of convenience-oriented businesses proves that people are willing to pay more for services that save them time.
9. Adopt a long-term perspective.
Respondents rated their overall satisfaction significantly lower on a historical basis than on the survey date itself. And, although daily satisfaction improved as the study progressed, historical satisfaction did not. It evidently takes a tremendous number of "good days" before customers' historical opinions change. Managers must take a long-term approach when attempting to improve perceptions.
10. Never underestimate the power of a friendly server.
Although waiting is an issue worth addressing, managers
should not lose perspective. Servers should continually be trained and
rewarded for good service, since their efforts can overcome many negative
effects of waiting.